Один корень
Объяснение:
Левая часть - положительна , значит положительна и правая ,
то есть x > 0 , но тогда функция , стоящая в левой части - возрастает
( как сложная функция , составленная их двух возрастающих ) , а в
правой части - убывающая функция , значит уравнение может иметь не
более одного корня ;
Функция y =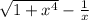 
непрерывна при x > 0 ;
y ( 0,1 ) =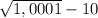 
< 0 ; y (1) = 
⇒
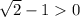на интервале ( 0 ; 1 ) y (x) имеет корень и как доказано он
единственный
Это арифметическая прогрессия.
a1 = 1; d = 1; любое a(n) = n.
Нужно найти такое n, что S(n) <= 235; S(n+1) > 235.
{ S(n) = (a1 + a(n))*n/2 = (1 + n)*n/2 <= 235
{ S(n+1) = (a1 + a(n+1))*(n+1)/2 = (1 + n + 1)(n + 1)/2 > 235
Получаем
{ (n + 1)*n <= 470
{ (n + 2)(n + 1) > 470
Раскрываем скобки
{ n^2 + n - 470 <= 0
{ n^2 + 3n - 468 > 0
Решаем квадратные неравенства
{ D = 1 + 4*470 = 1881 ≈ 43,4^2
{ D = 9 + 4*468 = 1881 ≈ 43,4^2
Как ни странно, дискриминанта получились одинаковые.
{ n = (-1 + 43,4)/2 <= 21
{ n = (-3 + 43,4)/2 > 20
ответ 21.
Это диофантово уравнение первой степени.
НОД (5,3) = 1 - уравнение имеет множество решений.
Оно описывается, соответственно, следующей системой двух кравнений:
х = 1 - 3n
y = 2+5n, где n - целое число.
Чтобы найти частные решения, нужно вместо n в данную систему подставлять по очереди 1, 2, 3, 4, 5 и т.д.
При n = 1 x = 1-3 = -2, y = 2+5 = 7. Пара чисел -2 и 7 является частным решением уравнения в целых числах.
При n = 2 x = 1 - 3*2 = 1 - 6 = -5, y = 2+5*2 = 2+10 = 12. Пара чисел (-5) и 12 является частным решением данного уравнения в целых числах.
Таким образом, подставляя вместо n любое целое число, вы найдете несколько частных решений.