(см. объяснение)
Объяснение:
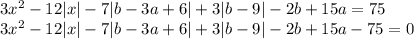
Введем функцию  .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке 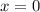 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров  и
и 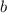 .
.
Уравнение  может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 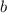 только, если
только, если 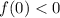 .
.
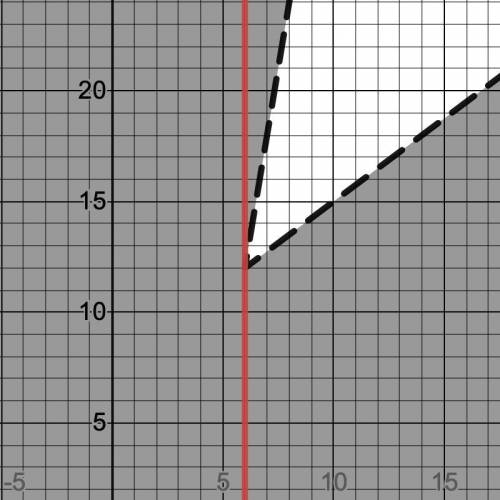
Тогда перейдем к неравенству:
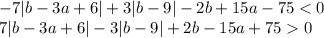
Построим его в координатах 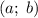 .
.
(см. прикрепленный файл)
Получили, что при 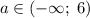 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 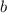 .
.
ответим теперь на вопрос задачи: ниже 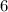 .
.
Задание выполнено!
Объяснение:
2A . 15 . . . . = [( a² + b² - ( a - b )²]/( a² - b²) =( a² + b²- a²+ 2ab- b²)/(a² - b²) =
= 2ab/( a² - b²) .
16 . . . . = [( a - b )²- ( a + b )²]/( a² - b²)] = ( a²- 2ab + b²- a²- 2ab -b²)/(a² - b²) =
= - 4ab/( a² - b²) ;
17 . . . . = ( 4x - 4x + 4y )/( x² - y² ) = 4y/( x² - y² ) ;
18 . . . . = [ 3y² * 3( x - y ) ]/[ ( x² - y² )y ] = 9y/( x + y ) ;
19 . . . . = [ ( x² - y² ) * 2y ]/[ 2xy( x - y ) ] = ( x + y )/x ;
20 . . . . = ( x² - y²)/ y² : ( 7x - 7y )/y = ( x² - y²)/ y² * y/7( x - y ) = ( x + y )/7y .
1) x1= -0.5; x2=-1.
2) x1=1.5; x2=1.5.
Объяснение:
1) 2х² + 3х +1 =0 ;
a=2; b=3; c=1;
D=b²-4ac=3²-4*2*1=9-8=1>0 - два корня
x1=(-b+√D)/2a=(-3+1)/2*2 =-2/4=-0.5
x2=(-b-√D)/2=(-3-1)/4=-4/4= -1;
x1= -0.5; x2=-1.
***
2) 4х²-12х+9=0;
a=4; b=-12; c=9;
D=b²-4ac=(-12)²-4*4*9=144-144=0 - два равных корня.
x1=1.5; x2=1.5.