Объяснение:
таблица :
X 0 2
y 3 8
.............
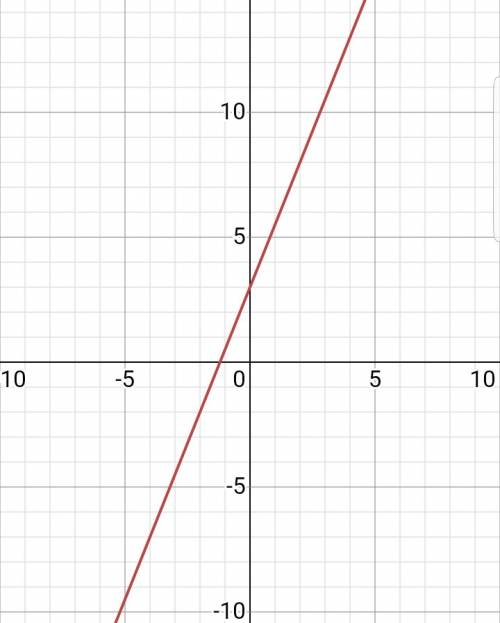
(РИС.1)
Корнями (нулями) являются значения x, в которых график пересекает ось абсцисс (ось X). Для определения корней (нулей) подставляем 0 вместо y и решаем относительно x. Х1= 3, Х2= 1.
Построим график параболы, используя направление ветвей, вершину, фокус и ось симметрии.
Направление: направлено вверх
Вершина: (2,−1)
Фокус:
(2,−3/4).
Ось симметрии:
x=2
Направляющая:
y=−5/4
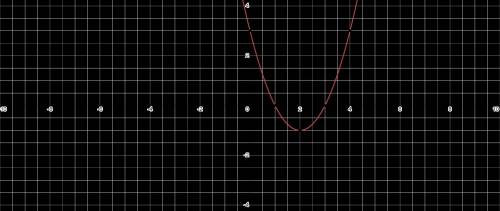
x 0 1 2 3 4
y 3 0 −1 0 3
(РИС.2)
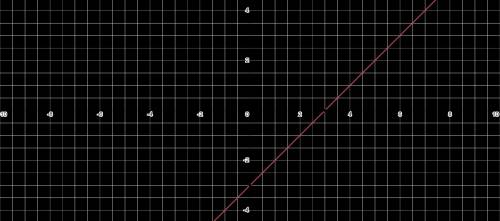
Построим прямую с углового коэффициента и пересечения с осью Y или опираясь на две точки.
Угловой коэффициент: 1
Пересечение с осью Y: (0,−3)
x 0 3
y −3 0
Объяснение:
Пример 1. В урне 10 белых и 8 черных шаров. Наудачу отобраны 5 шаров. Найти вероятность того, что среди них окажется ровно 2 белых шара.
Подставляем в формулу (1) значения: K=10K=10, N−K=8N−K=8, итого N=10+8=18N=10+8=18, выбираем n=5n=5 шаров, из них должно быть k=2k=2 белых и соответственно, n−k=5−2=3n−k=5−2=3 черных. Получаем:
P=C210⋅C38C518=45⋅568568=517=0.294.P=C102⋅C83C185=45⋅568568=517=0.294.
Пример 2. В урне 5 белых и 5 красных шаров. Какова вероятность вытащить наудачу оба белых шара?
Здесь шары не черные и белые, а красные и белые. Но это совсем не влияет на ход решения и ответ.
Подставляем в формулу (1) значения: K=5K=5 (белых шаров), N−K=5N−K=5 (красных шаров), итого N=5+5=10N=5+5=10 (всего шаров в урне), выбираем n=2n=2 шара, из них должно быть k=2k=2 белых и соответственно, n−k=2−2=0n−k=2−2=0 красных. Получаем:
P=C25⋅C05C210=10⋅145=29=0.222.P=C52⋅C50C102=10⋅145=29=0.222.
Пример 3. В корзине лежат 4 белых и 2 черных шара. Из корзины достали 2 шара. Какова вероятность, что они одного цвета?
Здесь задача немного усложняется, и решим мы ее по шагам. Введем искомое событие
A=A= (Выбранные шары одного цвета) = (Выбрано или 2 белых, или 2 черных шара).
Представим это событие как сумму двух несовместных событий: A=A1+A2A=A1+A2, где
A1=A1= (Выбраны 2 белых шара),
у =5.5х ху =5.5
Объяснение:
решиние на +