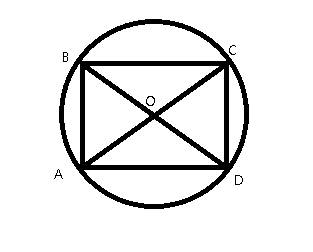
Т.к. Углы у него прямые, то стороны, имеющие одинаковые буквы, перпендикулярны, а другие - параллельны. Рассмотрим два треугольника: AOB и COD. Углы AOB и COD равны, (вертекильные), ABO=CDO( накрест лежащие), DCO=BAO( смежные).=> треугольники AOB и COD подобны. Но нам известно, что в AB и CD параллельны и заключены между двумя параллельными прямыми =>AB = CD =>треуг. AOB и COD равны=>AO=CO. Если проделать то же самое с другими треугольниками, (BOC и AOD), то докажете, что все 4 отрезка равны, и поэтому откуржность, лежащяя в точке пересечения диагоналей и имеющая радиус рывный одному из отрезков, будет пересекать концы остальных трех =>лежать на всех 4 углах прямоугольника.
Пусть х-общее число шаров, тогда х/2 шаров осталось в конце представления, также поскольку перед началом представления было 3х/7 шаров, а потом продали ещё 15, составим и решим уравнение:
х/2=х-(3х/7+15) Рассмотрим отдельно правую часть
х-(3х/7+15)= Приведём к общему знаменателю всю правую часть
=(7х-3х-105)/7=(4х-105)/7 Подставим это в уравнние
х/2=(4х-105)/7 Решим как пропорцию
7х=2(4х-105)
7х=8х-210
-х=-210
х=210
ответ:210 шаров.