Для начала найдем разность арифмитической прогрессии
по формуле :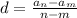
an и am это какие та два не последовательных члена арифмитической прогрессии , в нашем случае у нас an=a20 am=a4
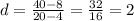
теперь когда известна разность узнаем чему равен первый член прогрессии по формуле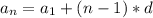
вместо an подставим уже известный четвертый член арифмитической прогрессии
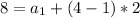
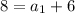
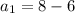
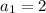
теперь найдем шестой член прогрессии
по той же формуле
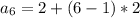
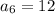
Объяснение:
ответ:
судебник 1497 года — свод законов государства.
содержание судебника распадается на четыре части:
деятельность центрального суда и нормы уголовного права (ст.1-36).
организация и деятельность местных судов (ст. 37-45).
гражданское право и гражданский процесс (ст. 46-66) (наследование, договоры личного найма, купли-продажи, переход крестьян от одного хозяина к другому, о холопстве).
дополнительные статьи по судебному процессу (ст.67-68)
объяснение:
подробнее можете прочитать тут
x=125 (детский)
y=190 (взрослый)
объяснение:
2х+y=440;
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим:
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=755
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755-3x+4x=-755+880
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755-3x+4x=-755+880x=125 (детский)
2х+y=440; 3x+2y=755 - это сис-ма ур-ний, методом гаусса выразим y через x и получим: y=440-2x, заменим: 3x+2(440-2x)=7553x+880-4x+755-3x+4x=-755+880x=125 (детский)y=190 (взрослый)
a6=12
——————————————