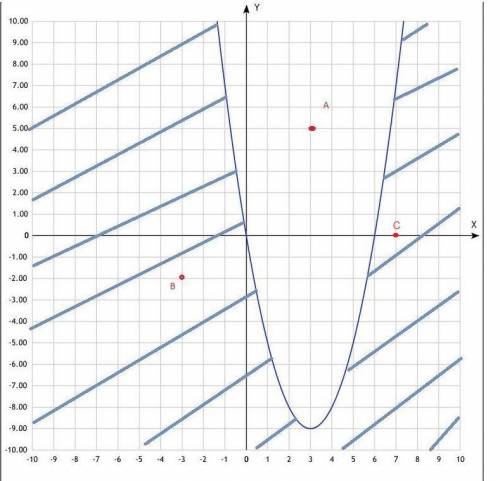
судя по заданию-график построен y=x^2-6x
решением неравенства
y<=x^2-6x- будет внешняя часть параболы, включая саму параболу. Если вы затрудняетесь с ее определением-совет: берите точку C (7;0) и подставляйте в неравенство
0<=49-42-верно. значит внешняя часть параболы, куда входит C (7;0)-решение. Сама парабола тоже решение- так как неравенство нестрогое. Область решения неравенства выделили штриховкой . как показано на чертеже.
По поводу точек А и В -поставлю их в плоскости рисунка.
А входит во внутреннюю область параболы-значит не является решением, В-во внешнюю, область штриховки, значит решение неравенства.
Функция у(х), график которой симметричен относительно
прямой х=3, должна обладать свойством у(х)=у(6-х), это -
чётность относительно сдвинутой переменной t=x-3.
2*p*x^2 - (p-11)*x + 17=2*p*(6-x)^2 - (p-11)*(6-x) + 17.
После раскрытия скобок и приведения подобных, получаем
условие: (p+1)(x-6)=0. Чтобы это было верно при любых х,
надо: р= -1. Это и есть ответ.