105. а > 12
106. РЕШЕНИЙ НЕТ
....
108. с = 2
Объяснение:
105.

Найти значения а, при которых
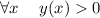
Графиком функции является парабола, ветви вверх. Необходимо вычислить такие значения а, при которых вершина параболы находится выше оси Ох.
Найдем через производную координату х точки минимума функции
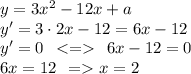
и координату у
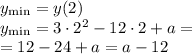
И найдем значения а, при которых у(мин) >0
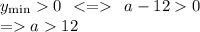
106. Решений нет. См. в фотографии.
Элементарно приводится контрпример.
Для любых значений а
значение функции при х = 0
будет равно 2 - т.е. положительное.
Что противоречит условиям
108.
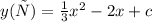
На самом деле здесь оптимально будет решить систему.
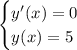
Но поступим иначе.
График функции - парабола, ветви вниз.
1) Минимальное значение у - в точке вершины параболы. Т.е. в точке, где производная функции равна 0:
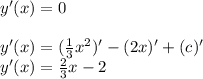
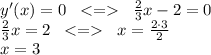
2) И в этой точке значение у Должно быть равно 5
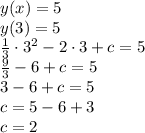
ответ: при с = 2

А в следующем месяце было тоже самое - воскресенье было последним днём месяца. Это значит, что второй месяц был невисокосный февраль, а первый январь.
Итак, 31 января Игорь был в Мурманске, а 31-7=24 января в Новосибирске.
В следующем месяце, феврале, 28 он был в Томске, а за неделю до этого, 21 февраля в Кирове.
Остаётся добавить, что последний раз 31 января и 28 февраля выпали на воскресенье в 2010 г.