Допустим, что 
. Тогда имеем уравнение 
, не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.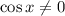 
Преобразуем правую часть:
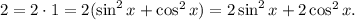
Перенесем все влево с противоположным знаком:
Поскольку 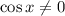, можем разделить обе части уравнения на 
. В итоге имеет равносильное исходному уравнение
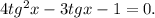
Заметим, что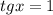 
является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен 
.
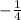Соответственно, имеем два случая: или 
или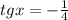 
.
1 случай.
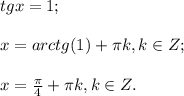
2 случай.
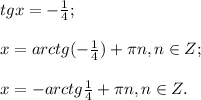
Имеем две серии корней.
ОТВЕТ: π/4 + πk, k ∈ Z; -arctg(1/4) + πn, n ∈ Z.
task/29760192 cos(3x/2)*cos(x/2) -1 > (1/2) * (1 -√3) *cosx
Решение : cos(3x/2)*cos(x/2) -1 > (1/2) * (1 -√3) *cosx ||*2||
2cos(3x/2)*cos(x/2) -2 > (1 -√3) *cosx ;
cos2x+cosx - (1 -√3) *cosx - 2 > 0 ;
2cos²x -1 +cosx - cosx +(√3) *cosx - 2 > 0 ;
2cos²x +(√3) *cosx -3 >0 ⇔ ( cosx +√3 )(2cosx -√3 ) >0 ||cosx +√3 >0 ||⇔ cosx > (√3) /2 ⇒ 2πn - π / 6 < x < π / 6 + 2πn , n ∈ ℤ (объединение интервалов )
ответ : x ∈ ( - π / 6 + 2πn ; π / 6 + 2πn ) , n ∈ ℤ.
P.S. 2cos²x +(√3) *cosx -3 = 0. D=(√3)²+4*2*(-3) =27 =(3√3)² ⇒√D =3√3)
cosx₁ = - √3 < - 1 → посторонний корень ; cosx₂ =(√3) / 2. * * *