У треугольника вершины три. Значит, в любом случае, на одной из прямых будут лежать две вершины. Очевидно, что тогда все треугольники разделятся на два класса, те у которых две вершины на первой прямой, и те, у которых - на второй. Выбрать две точки из 12 можно числом сочетаний. На каждые такие точки приходится 13 возможных третьих вершин.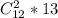 
. (Аналогично для другой прямой) 
- треугольников.
Четырехугольник имеет четыре вершины, потому имеет смысл рассматривать один их класс (ведь на каждой прямой может быть только две вершины (ибо у четырехугольника три вершины не могут лежать на одной прямой)) Выбрать первые две можно так: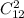 
, каждой такой паре соответствует 
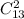пар вершин на второй стороне. тогда прямоугольников 
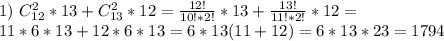
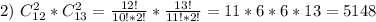
на нуль делить нельзя
число в модуле не может быть отрицательным
Объяснение:
например
1) при х=-8
если отрицательное значение записать в модуле то оно станет положительным и таким образом 8:(-8)=-1
2) при х=-5
если отрицательное значение записать в модуле то оно станет положительным и таким образом 5:(-5)=-1
3) при х=1
число изначально положительное и поэтому если записать его в модуле то его значение не изменится т.е он так и будет оставаться 1
1:1=1
4) при х=7
число изначально положительное и поэтому если записать его в модуле то его значение не изменится т.е он так и будет оставаться 7
7:7=1
5) при х=128
число изначально положительное и поэтому если записать его в модуле то его значение не изменится т.е он так и будет оставаться 128
128:128=1
6) при х больше нуля
в таком случае нам надо взять самое наименьшее число которое больше нуля т.е это число 1 исходя от этого получается что 1:1=1 (можно взять другие числа)
надеюсь что
хорошего дня