Перепишите текст, раскрывая скобки, вставляя, где это необходимо, пропущенные
буквы и знаки препинания.
с (не)запам...тных времен человек употребля...тв пищу (дико )р..стущие плоды и
ягоды обладающие (не)повт..римымар..матом. Клюква брусника черника малина
земляника наст... Ящиекл...довые в...таминов. В Ш. .Повнике содержится больше
B..тамина С чем в лимонах и ап..льсинах авр...бине в..тамина А больше, чем в
М.ркови.
Собрать плоды следу..Тв сухую погоду. Собра..ые влажными они портят..ся. Ягоды
сорва...ые в жаркую погоду быстро вянут так как содерж..т мен..ше сока.
(Не)льзясобрать (не)созревшие ягоды, лучше оставить их д.. зреть, чтобы) они
нал..лись соком и набрали найбольш..е кол..ичество в..таминов. (Не) соб..райте
загнившие(3) ягоды так как они (не) содержат цен..ых веществ и могут быть пр..чиной
порчи сырья.
При сбор.. ягод буд..теост..рожны и ак..уратныcт..райтесь (не) т.птать ягодные
куст..ки.
Сушите плоды в печах предварительно провялив на сонце(4). Чтобы) ягоды (не)
подгрели(2) и (не) сл..жались на сонце их (не)обходимо пер..мешивать. Сушен...ые
ягоды пр..меняются в основном как л..карство.
задание:
1)Горизонтальная схема сложных предложений. 2)Определить вид придаточного.
3)Синтаксический разбор первого предложения
1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.
Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.
А значит ответ нет.
2) Заметим, что искомая сумма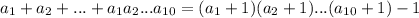
.
И правда. Пусть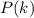
- сумма всех комбинаций по 1 ... по k элементов. Тогда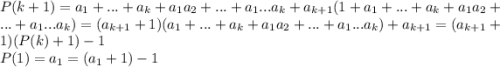 
Т.к. числа отрицательны, то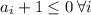
Если хотя бы одно из
, вся сумма равна -1.
В остальных случаях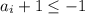
- всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что 
.
А тогда сумма могла равняться только -1