Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.
x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).
График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).
Четная функция: f(-x)=f(x) для всех ;
Нечетная функция: f(-x)=-f(x) для всех ;
График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
По свойству арифметической прогрессии:
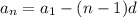
У нас известно 2 члена арифметической прогрессии, составим из них систему и найдем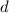 
и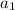 
:
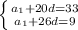
Выражаем ихз первого 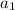и получаем:
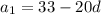
Подставляем во второе и получаем:
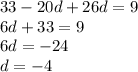
Подставляем d в выражение для 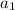и получаем:
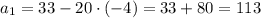
Теперь напишем формулу для суммы n членов арифметической прогрессии:
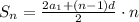
теперь подставляем в это выражение найденные числа и получаем:
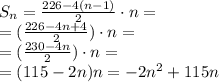
Получилась функция, которая зависит от n.
Нужно найти ее максимум:
Поскольку это парабола ветви которой направлены вниз (потому что перед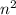 
стоит отрицательный коэффициент), то максимумом у нее будет точка, где производная принимает значение равное 0.
Найдем производную по n от этой функции:
Получим:
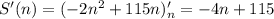
Теперь надо найти где она равно 0.
Решаем уравнение: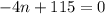 
получаем: 
Теперь осталось выяснить какое n нам взять. n=28 или n=29.
Для этого надо просто вычислить значение суммы при n=28 и при n=29
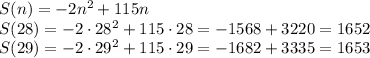
Как мы видим S(29)>S(28),
значит при n=29 сумма принимает максимальное значение равное 1653
ответ: максимальное значение суммы первых n членов арифметической прогрессии равно 1653 и достигается при n=29
a)-9a+18b-36c= 9(-a+2b-4c)
-9a+18b-36c= 3*3(-a+2b-4c)
b)12m-18n-42p= 6(2m-3n-7p)
12m-18n-42p= 3*2(2m-3n-7p)
Объяснение: