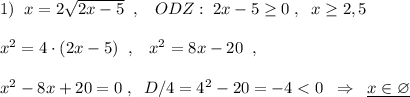
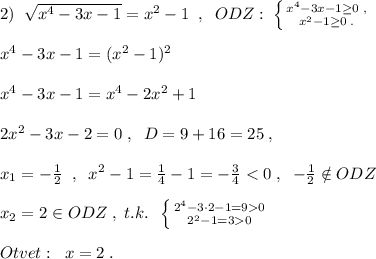
1. x=2√(2x-5) ОДЗ уравнения 2х-5≥0 x≥2.5; возведем в квадрат обе части
х²=4*(2х-5); х²-8х+20=0; Дискриминант Д=64-80=-16<0; корней нет.
2. √(x⁴-3x-1)=x²-1, Возведем обе части в квадрат, x⁴-3x-1=x⁴-2х²+1;
2х²-3х-2=0, х₁,₂=(3±√(9+16))/4=(3±5)/4; х₁=2; х₂=-0.5
При возведении в четную степень могли появиться посторонние корни.
Поэтому проверка. х₁=2; √(2⁴-3*2-1)=2²-1,√9=4-1; 3=3, Вывод х₁=2 - корень исходного уравнения.
х₂=-0.5; √((-0.5)⁴-3*(-0.5)-1)=(-0.5)²-1; √(0.0625+1.5-1)=0.25-1, ; 0.75=-0.75 Вывод х₂=-0.5- не является корнем исходного уравнения.
ответ 2
Если в уравнении рассматриваются частные случаи sinx=0 и cosx=0, то пользуются более простыми формулами, и пользуются периодом П, так как нули синуса и косинуса повторяются через период, равный П, хотя в общем случае наименьший положительный период для этих функций равен 2П.
sinx=0, x=πn
cosx=0, x=π/2+πn
В общем случае sinx=a, x=(-1)^n*arcsina+πn и в случае sinx=0 можно было бы записать
х=(-1)^n*arcsin0+πn=(-1)^n*0+πn=πn.
Если решаем ур-ие sinx=1, то x=π/2+2πn - частный случай, а в общем случае писали бы х=(-1)^n*arcsin1+πn=(-1)^n*π/2+πn - ,более сложный вид, но правольная запись.
sinx=-1 x=-π/2+2πn - частный случай
Если cosx=a,то х=±arccosa+2πn.Можно для ур-ия cosx=0 записать решение через общую формулу х=±arccos0+2πn=±π/2+2πn (это более сложная запись, но правильная)
cosx=1, x=2πn
cosx=-1, x=π+2πn
Для уравнений tgx=a, x=arctga+πn
ctgx=a, x=arcctga+πn
Итак, если использовать общие формулы, то период только для косинуса берём 2πn. а для остальных функций используем πn.