Есть функция y=√(x-5). Надо проверить принадлежат ли ее графику какие-либо точки. Для этого подставляем значение х этой точки в фунцию и смотрим каким получится значение у. Если оно совпадет со значением у проверяемой точки, то точка принадлежит гарфику, если не совпадет, то не не принадлежит.
а) точка (9;2) подставляем в функцию 9 и смотрим получится 2 или нет. y=√(9-5)=√4=2 - точка (9;2) принадлежит графику функции y=√(x-5)
б) точка (1;2) подставляем в функцию 1 и смотрим получится 2 или нет. y=√(1-5)=√(-4) квадратный корень из отрицательного числа вычислить нельзя. Точка (1;2) не принадлежит графику функции y=√(x-5)
в) точка (5;1) подставляем в функцию 5 и смотрим получится 1 или нет. y=√(5-5)=√0=0≠1 - точка (5;1) не принадлежит графику функции y=√(x-5)
г) точка (1;-√6) подставляем в функцию 1 и смотрим получится -√6 или нет. y=√(-1-5)=√(-6) квадратный корень из отрицательного числа вычислить нельзя. Точка (1;-√6) не принадлежит графику функции y=√(x-5)
Как перевести бесконечную периодическую десятичная дробь в обыкновенную: Целое число не изменяется, в дробь переводится то, что после запятой. В числитель обыкновенной дроби нужно записать разность между всем числом после запятой и числом после запятой до периода, а в знаменатель число из «девяток» и «нулей», причем, «девяток» столько, сколько цифр в периоде, а «нулей» столько, сколько цифр после запятой до периода. Всё число после запятой 52, число до периода - 5. Цифр в периоде одна, цифр ДО периода - одна. Число 3,5(2)=3 (52-5)/90 = 3⁴⁷/₉₀ Проверим: 47:90=0, 52222222, т.е. 0, 5(2)
а) 5*5*5*5
б) -3*(-3)*(-3)
-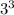 = -27
= -27