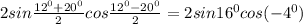Question

Представьте в виде произведения: 1)sin 12°+sin 20°= 2)sin 52°-sin 32°= 3)cos π\10 - cos π\20= 4)sin π\6 - sin π\9= 5)sin a - sin (a+ π\3)=

Answer 1

1) $2 sin\frac{12^{0}+20^{0}}{2}cos\frac{12^{0}-20^{0}}{2}=2sin16^{0}cos(-4^{0})$

Answer 2

1) Для решения данного уравнения, мы будем использовать формулу синуса суммы углов:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)

Используя эту формулу, мы можем переписать уравнение следующим образом:
sin 12° + sin 20° = sin(12° + 20°) = sin 32°

Таким образом, ответ на это уравнение равен sin 32°.

2) Для данного уравнения, мы также будем использовать формулу синуса суммы углов:
sin(a - b) = sin(a)cos(b) - cos(a)sin(b)

Используя эту формулу, мы можем переписать уравнение следующим образом:
sin 52° - sin 32° = sin(52° - 32°) = sin 20°

Таким образом, ответ на это уравнение равен sin 20°.

3) Для решения данного уравнения, мы будем использовать формулу разности косинусов:
cos(a - b) = cos(a)cos(b) + sin(a)sin(b)

Используя эту формулу, мы можем переписать уравнение следующим образом:
cos π/10 - cos π/20 = cos(π/10 - π/20) = cos π/20

Таким образом, ответ на это уравнение равен cos π/20.

4) Для данного уравнения, мы также будем использовать формулу разности синусов:
sin(a - b) = sin(a)cos(b) - cos(a)sin(b)

Используя эту формулу, мы можем переписать уравнение следующим образом:
sin π/6 - sin π/9 = sin(π/6 - π/9) = sin π/18

Таким образом, ответ на это уравнение равен sin π/18.

5) Для решения данного уравнения, мы будем использовать формулу разности синусов:
sin(a - b) = sin(a)cos(b) - cos(a)sin(b)

Используя эту формулу, мы можем переписать уравнение следующим образом:
sin a - sin (a + π/3) = sin(a)cos(π/3) - cos(a)sin(π/3) = sin(a) * 1/2 - cos(a) * √3/2

Таким образом, ответ на это уравнение равен sin(a) * 1/2 - cos(a) * √3/2.