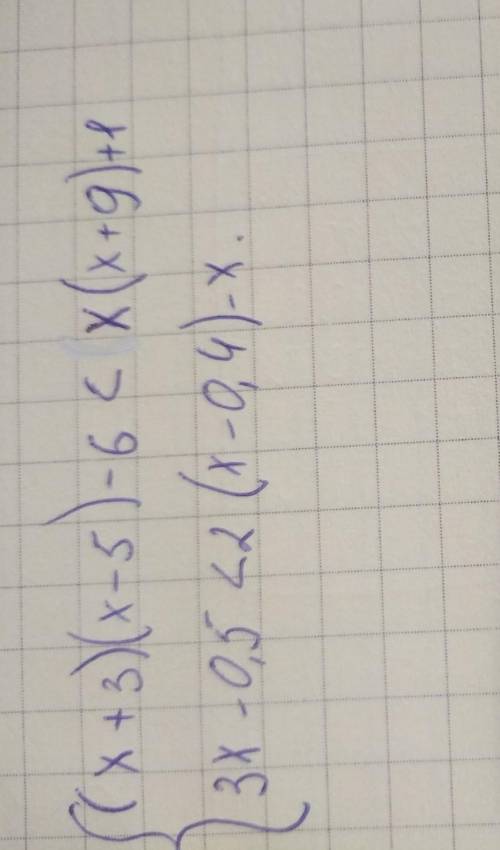
1)
а) Д= 25+96=121
x1= (-5+11)/2=3
х2= (-5-11)/2=-13
б) Д= 361+168=529
х1= (19+23)/6=7
х2=(19-23)/6= 4/6
2)a) x^2 -14x +49 = (x-7)^2
б) x^2 + 5x -6 = (x+5)^2 -5x -31
в)
3)x^2 -4x +31>0
Д=16-4*31 < 0 => нету пересечения с осью ox, т.к. ветви вверх, то всегда >0
б) 9x^2 +24x +16
Д= 576-576=0 => 1 т. пересечения с осью ox, ветви вверх => >=0
5) 4x^2 -x = x(4x-1)
б) x^2 +7x+10
Д=49-40=9
x1= -7+3/8= -1/2
x2= -5/4
x^2+7x+10=(x+1/2)(x+5/4)
В) 5x^2 - 7x +2
Д= 49-40=9
x1 = 7+3/10=1
x2= 7-3/10= 4/10=0,4
5x^2 - 7x +2 = 5(x-1)(x-0,4) про 5 не уверен
Г) -2x^2-9x-9=2x^2 + 9x +9
Д=81-72=9
x1= -9-3/4=-3
x2=-9+3/4= -6/4
2x^2 + 9x + 9 = 2(x+3)(x+6/4) про 2 не уверен :C
1:2 = x:2x
третье число 63-x-2x = 63-3x
произведение : x * 2x * (63-3x) представим в виде функции
y=x * 2x * (63-3x) = 126x^2 -6x^3
y = 126x^2 -6x^3 (1)
найдем экстремум функции
производная
y' = (126x^2 -6x^3)' = 252x - 18x^2
приравниваем к нулю
0 = 252x - 18x^2 = 18x * (14-x)
произведение равно нулю,если один из множителей равен нулю
x = 0 - не подходит
или
14-x =0 ; x =14
подставим в уравнение
y = 126*14^2 -6*14^3 = 8232
тогда искомые числа
x : 2x = 14 : 28
третье число
63 - 14 - 28 = 21
сумма 14+28+21 =63
произведение 14*28*21 =8232
ответ 14+28+21 =63