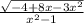

D(f) = [2/3; 1) U (1; 2]
Объяснение:
для того, чтобы определить D(f), нужно разделить выражение и рассмотреть каждый случай отдельно.
1. 1) нули функции
x² - 1 ≠ 0, откуда
x - 1 ≠ 0, x + 1 ≠ 0, x ≠ ± 1
отсюда: область определения: x ∈ R
2) - 4 + 8x - 3x²
-3x² + 8x - 4 ⩾ 0
3x² - 8x + 4 ⩾ 0
D = 64 - 12 × 4 = 16
x1 =
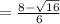
x1 =
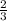
x2 =
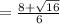
x2 = 2
x ∈ [2; +∞) U [2/3; +∞)
2. находим пересечение, необходимое, чтобы функция соблюдалась:
1) x ∈ (1; +∞) U [2; +∞)
x ∈ (1; 2]
2) x ∈ (1; +∞) U [2/3; +∞)
x ∈ [2/3; 1)
ОДЗ: х принадлежит (-бесконечность; -4) U (4; +бесконечность)
для нахождения экстремума нужно найти производную...
f ' (x) = ((2x-5)(x+4) - (x^2-5x)) / (x+4)^2 = (2x^2 + 3x - 20 - x^2 + 5x) / (x+4)^2 =
= (x^2 + 8x - 20) / (x+4)^2 = (x-2)(x+10) / (x+4)^2
решение неравенства (x-2)(x+10) / (x+4)^2 > 0 (корни: -10; -4; 2)
х принадлежит (-бесконечность; -10) U (2; +бесконечность) =>
функция возрастает при х принадлежит (-бесконечность; -10] U [2; +бесконечность)
функция убывает при х принадлежит [-10; -4) U (-4; 2]
при х = -10 ---функция достигает максимума fmax = (100+50)/(-6) = -25
при х = 2 ---функция достигает минимума fmin = (4-10)/6 = -1
система:
9x - x^2 > 0
5 - x > 0
lg(5-x) не равен 0
x(9 - x) > 0
x < 5
5 - x не равно 1
х принадлежит (-бесконечность; 0) U (9; +бесконечность)
х принадлежит (-бесконечность; 5)
х не равен 4
х принадлежит (-бесконечность; 0) --- x < 0
ОДЗ: х принадлежит (-бесконечность; -4) U (4; +бесконечность)
для нахождения экстремума нужно найти производную...
f ' (x) = ((2x-5)(x+4) - (x^2-5x)) / (x+4)^2 = (2x^2 + 3x - 20 - x^2 + 5x) / (x+4)^2 =
= (x^2 + 8x - 20) / (x+4)^2 = (x-2)(x+10) / (x+4)^2
решение неравенства (x-2)(x+10) / (x+4)^2 > 0 (корни: -10; -4; 2)
х принадлежит (-бесконечность; -10) U (2; +бесконечность) =>
функция возрастает при х принадлежит (-бесконечность; -10] U [2; +бесконечность)
функция убывает при х принадлежит [-10; -4) U (-4; 2]
при х = -10 ---функция достигает максимума fmax = (100+50)/(-6) = -25
при х = 2 ---функция достигает минимума fmin = (4-10)/6 = -1
система:
9x - x^2 > 0
5 - x > 0
lg(5-x) не равен 0
x(9 - x) > 0
x < 5
5 - x не равно 1
х принадлежит (-бесконечность; 0) U (9; +бесконечность)
х принадлежит (-бесконечность; 5)
х не равен 4
х принадлежит (-бесконечность; 0) --- x < 0
х€[2/3;1)U(1;2]
Объяснение:
1. Данное выражение неопределено при значениях х, обращающих его знаменатель в 0. Найду нули знаменателя:
х^2-1=0; х1=1, х2=-1
2. Данное выражение не определено, если подкоренное выражение отрицательно. Найду область определения:
-4+8х-3х^2>=0,
3х^2-8х+4<=0, Найду нули:
3х^2-8х+4=0, D=4^2-3×4=4,
x1=(4+2)/3=2, x2=(4-2)/3=2/3
х€[2/3;2]-решение неравенства.
3. Первое и второе условия должны соблюдаться одновременно, значит:
х€[2/3;1)U(1;2]