В одной коробке в 3 раза меньше чем во второй. После того как в первую коробку добавили 8 кг конфет , а из второй убрали 6 кг конфет, в обеих коробках стало поровну. Сколько кг конфет было в каждой коробке первоначально?
ответ: 7 кг ; 21 кг
Объяснение: Пусть в конце в обеих коробках стало x кг конфет
Следовательно в первой коробке первоначально было (x - 8 ) кг конфет , а во второй (x+6) кг конфет. Можем составить уравнение :
3(x - 8 ) = x + 6 ⇔ 3x -24 = x + 6 ⇔ 3x - x = 6+24⇔ 2x =30 ⇔ x= 15 .
в первой коробке первоначально было (x - 8 ) кг = (15-8) кг =7 кг ;
во второй коробке: (x + 6 ) кг= (15 + 6) кг = 21 кг .
ответ: 35
Объяснение:
Предположим, что в классе менее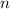 
человек, причем 
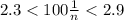,тогда минимальный процент неуспевающих учеников будет достигнут при наибольшем возможном числе учеников, то есть 
и при минимальном числе неуспевающих учеников, то есть 
.
Таким образом, при таком условии процент неуспевающих учеников :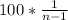 
Найдем минимальное число 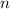удовлетворяющее неравенству:
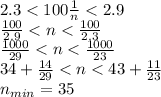
Предположим, что в классе менее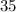 
человек, тогда минимальный процент учеников неуспевающих в классе
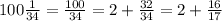
Сравним:
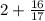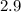
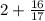и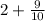 
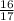и 
и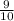 
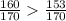
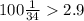
То есть мы пришли к противоречию. А значит в классе как минимум 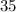человек. C другой стороны, как было показано выше, для случая 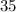человек может быть достигнут процент неуспевающих учеников в пределах от 2,3% до 2,9%. Это произойдет когда в классе из 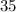человек неуспевает ровно ученик.
9
Объяснение:
Заметим, что 8 монет по 7 дадут нам в сумме 56, а если прибавить 5, то будет 61 - не подходит
тогда 7*7=49, 59-49=10=5*2 следовательно, нам понадобится 2+7=9 монет