Выражение a-(0,5a-10b)+(9b-2a) и вычислите его значение при a = - 2/5, b= -0,1

👇

Увидеть ответ

Ответ:

викусик152

02.03.2023

a - 0,5a + 10b + 9b - 2a = -1,5a + 19B

- 1,5 * (- 2\5) + 19 * (-0,1) = 3\5 - 1,9 = - 13\10 = -1.3

4,5(9 оценок)

Открыть все ответы

Ответ:

Kachelda

02.03.2023

наибольшее значение функции равно 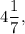$4\dfrac{1}{7} ,$ а наименьшее значение функции равно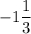 $-1\dfrac{1}{3}$

Объяснение:

Найти наибольшее и наименьшее значение функции

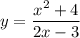$y=\dfrac{x^{2} +4}{2x-3}$ на промежутке [ 0; 5]

Так как делить на нуль нельзя, то 2х -3 ≠0, то есть х ≠ 1,5.

Тогда область определение функции: D(y) = ( -∞ ; 1,5 ) ∪(1,5; + ∞)

Найдем производную функции

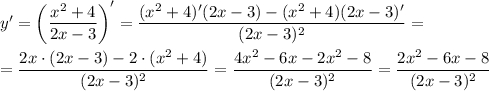
$y'=\left(\dfrac{x^{2} +4}{2x-3}\right)'= \dfrac{(x^{2} +4)'(2x-3) - (x^{2} +4)(2x-3)'}{(2x-3)^{2} } ==\dfrac{2x\cdot(2x-3) -2\cdot( x^{2} +4)}{(2x-3)^{2} } =\dfrac{4x^{2} -6x-2x^{2} -8}{(2x-3)^{2} } =\dfrac{2x^{2} -6x -8}{(2x-3)^{2} }$

Найдем критические точки, решив уравнение: y' = 0.

Дробь равна нулю, если числитель равен нулю

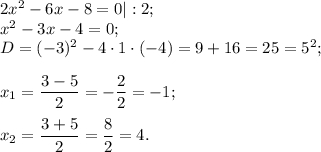
$2x^{2} -6x -8=0|:2;\\x^{2} -3x-4=0;\\D =(-3)^{2} -4\cdot1\cdot (-4)= 9+16=25 =5^{2} ;x{_1}= \dfrac{3-5}{2} =-\dfrac{2}{2} =-1;x{_2}= \dfrac{3+5}{2} =\dfrac{8}{2} =4.$

Заданному промежутку [ 0; 5] принадлежит х =4.

Найдем значение функции на концах промежутка и в точке х =4 .

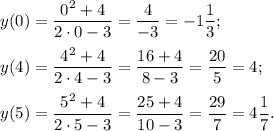
$y(0)=\dfrac{0^{2} +4}{2\cdot 0-3}=\dfrac{4}{-3} =-1\dfrac{1}{3} ;y(4)=\dfrac{4^{2} +4}{2\cdot4-3}=\dfrac{16+4}{8-3} =\dfrac{20}{5} =4;y(5)=\dfrac{5^{2} +4}{2\cdot5 -3}=\dfrac{25+4}{10-3} =\dfrac{29}{7} =4\dfrac{1}{7} .$

Сравним найденные значения и получим, что наибольшее значение функции равно 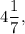$4\dfrac{1}{7} ,$ а наименьшее значение функции равно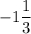 $-1\dfrac{1}{3}$

#SPJ1

4,6(28 оценок)

Ответ:

angrelygovo201

02.03.2023

Чтобы найти наибольшую скорость движения материальной точки, необходимо взять производную от функции s(t) по времени t и найти значения времени, при которых производная равна нулю. Затем, среди найденных значений выбрать наибольшее.

Дано:

s(t) = -t³ + 18t² - 60t

Чтобы найти скорость, возьмем производную s(t) по t:

v(t) = ds(t)/dt

v(t) = d/dt(-t³ + 18t² - 60t)

v(t) = -3t² + 36t - 60

Теперь найдем значения времени t, при которых производная равна нулю:

-3t² + 36t - 60 = 0

Для решения этого квадратного уравнения можно использовать квадратное уравнение или графический метод. Но в данном случае, можно заметить, что уравнение можно упростить, разделив все его члены на -3:

t² - 12t + 20 = 0

Это квадратное уравнение можно разложить на множители:

(t - 10)(t - 2) = 0

Отсюда получаем два значения времени: t = 10 и t = 2.

Теперь нужно выбрать наибольшее значение времени, чтобы найти наибольшую скорость. В данном случае, это t = 10.

Таким образом, наибольшая скорость движения материальной точки достигается при t = 10. Чтобы найти эту скорость, подставим t = 10 в выражение для скорости:

v(10) = -3(10)² + 36(10) - 60

v(10) = -3(100) + 360 - 60

v(10) = -300 + 360 - 60

v(10) = 0

Наибольшая скорость движения материальной точки равна 0.

4,4(86 оценок)

Это интересно:

Здоровье

10.07.2021

Голубые глаза: миф или реальность?...

Образование-и-коммуникации

21.09.2020