(см. объяснение)
Объяснение:
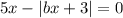
Самый верный решить любой параметр - это постараться построить его в координатах (b; x).
Попробуем применить этот прием здесь.
Сначала заметим, что при 
равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на 
.
Раскроем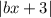 
:
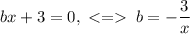
Видим гиперболу в координатах (b; x).
Построим ее и просчитаем знаки в областях, которые она образует, подставляя координаты соответствующих точек в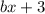 
.
Тогда при 
:
Строим фрагмент этого графика в определенных выше областях.
При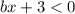 
:
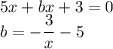
Тоже строим фрагмент этого графика в определенных выше областях.
Получим график уравнения:
(см. прикрепленный файл)
Итого:
При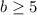
уравнение не имеет корней.При 
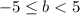уравнение имеет единственный корень.При 
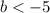уравнение имеет ровно два различных корня.Задание выполнено!
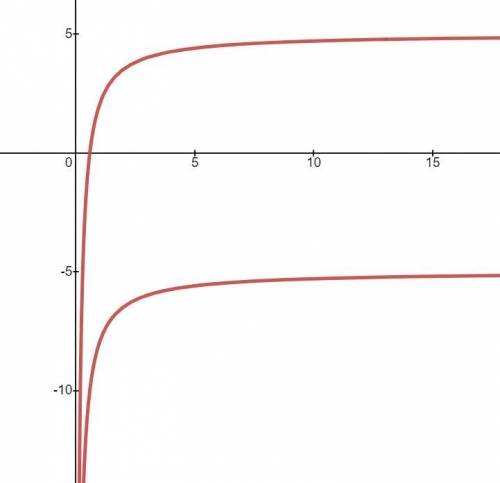
найдем координаты векторов АВ и АС, выходящих из вершины А, от координат конца вычтем координаты начала.
→АВ(4-3; 6-5); →АВ(1; 1); →АС(5-3; 5-5); →АВ(2; 0);
найдем длины этих векторов. длина →АВ равна √(1²+1²)=√2; длина →АС равна √(2²+0²)=2;
Найдем скалярное произведение этих же векторов. это сумма произведений соответствующих координат.
→АВ*→АВ=1*2+1*0=2
Разделим скалярное произведение векторов на произведение их модулей, найдя косинус угла между векторами.
2/(2√2)=√2/2, значит. внутренний угол при вершине А равен 45°
ответ 45°