38 см
Объяснение:
Пусть х см - одна из сторон прямоугольника, тогда (х + 5) см - другая сторона. Площадь прямоугольника равна 84 см².
Площадь находится по формуле S = ab, где a,b - стороны прямоугольника
х * (х + 5) = 84
х² + 5х = 84
х² + 5х - 84 = 0
D = 5² - 4 * 1 * (-84) = 25 + 336 = 361 = 19²
x₁ = (-5 - 19) / 2 = -24 / 2 = -12 ⇒ сторона не может быть отрицательна
x₂ = (-5 + 19) / 2 = 14 / 2 = 7
7 см - ширина прямоугольника
7 + 5 = 12 см - длина прямоугольника
Периметр находится по формуле P = 2 * (a + b), где a,b - стороны прямоугольника
2 * (7 + 12) = 2 * 19 = 38 см
![\displaystyle \sqrt[3]{2}= 2^{ \frac{1}{3} } \\ \displaystyle \sqrt[5]{3}= 3^{ \frac{1}{5} }](/tpl/images/0869/4658/e78b1.png)
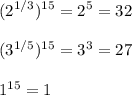
![\displaystyle \sqrt[3]{2} \ \textgreater \ \sqrt[5]{3}\ \textgreater \ 1](/tpl/images/0869/4658/44fe6.png)
Решим уравнение как квадратное уравнение относительно cos x.
Это однородное уравнение. Разделим левую и правую части уравнения на
Решая уравнение как квадратное уравнение относительно tg x, по теореме
Виета имеем, что
Решаем уравнение как квадратное уравнение относительно tgx
По формуле содержащего дополнительного угла, имеем что