
В рассматриваемом шестиразрядном числе abcdef, разряд “a” может принимать значения от 1 до 9 (9 значений), разряд “b” может принимать значения от 0 до 0 (1 значение), разряд “c” может принимать значения от 0 до 9 (10 значений), разряд “d” может принимать значения от 0 до 9 (10 значений), разряд “e” может принимать значения от 4 до 4 (1 значение), разряд “а” может принимать значения от 0 до 9 (10 значений).
Посчитаем всевозможное количество значений, которое может принимать число abcdef.
N=9*1*10*10*1*10=9000
Точно также посчитаем всевозможное количество значений, которое может принимать четырехзначное число wxyz, у которого разряд “w” может принимать значения 1 до 9 (9 значений), разряд “x” может принимать значения от 0 до 9 (10 значений), разряд “y” может принимать значения от 0 до 9 (10 значений), разряд “я” может принимать значения от 0 до 9 (10 значений).
M=9*10*10*10=9000
Как видим M=N. Число шестизначных чисел с двумя неизменяемыми разрядами равно числу четырехзначных чисел.


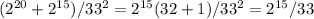
a) найдем корни квадратного трехчлена
x^2-10x+21=0x
2
−10x+21=0
по Виета
\begin{gathered}x_1=7\ \ \ \ \ \ x_2=3\\\ x^2-10x+21=(x-7)(x-3)\end{gathered}
x
1
=7 x
2
=3
x
2
−10x+21=(x−7)(x−3)
б) найдем корни квадратного трехчлена
\begin{gathered}5y^2+9y-2=0\\\ D=81+40=121\\\ x_1=\frac{-9+11}{10}=0,2 \ \ \ \ \ \ x_2=\frac{-9-11}{10}=-2\\\ 5y^2+9y-2=5(x-0,2)(x+2)\end{gathered}
5y
2
+9y−2=0
D=81+40=121
x
1
=
10
−9+11
=0,2 x
2
=
10
−9−11
=−2
5y
2
+9y−2=5(x−0,2)(x+2)