(5; 0)
Объяснение:
При пересечении графика функции с осью абсцисс (0х), координата «y» точки пересечения равна 0 (нулю).
Тогда:
0 = 3*x - 15
x = 5
ответ: (5; 0)
В обеих точках функция непрерывна
Объяснение:
Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.
для x = 0
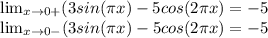
Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна
для x = 1
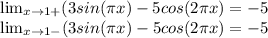
Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.
![Найти наибольшее и наименьшее значение функции y=x^3-6x^2+3 на отрезке [-2; 2]](/tpl/images/0895/1558/3827d.jpg)
ответ: 0=3*х-15 или 3*х=15 или х=15/3=5. Точка (5;0).
Объяснение: