8
Объяснение:
Найдём функцию Эйлера от числа 15. Это количество чисел, меньших 15 и взаимно простых с ним, то есть не имеющих с 15 общих делителей. Такими числами являются 1, 2, 4, 7, 8, 11, 13, 14, поскольку они не делятся ни на 3, ни на 5. Тогда функция Эйлера φ(15) = 8.
Так как 2 и 15 — взаимно простые числа, то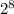 
сравнимо с 1 по модулю 15.
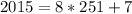
Тогда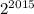 
можно записать в виде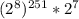 
Поскольку мы выяснили, что 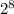сравнимо с 1 по модулю 15, то 
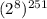также сравнимо с 1 по модулю 15.
Остаётся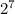 
, которое сравнимо с 8 по модулю 15, поскольку даёт остаток 8 при делении на 15.
То есть можем записать: 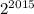≡ ≡ 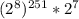≡ 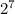8 mod 15
Это значит, что остаток равен 8.
Пёс Соколка живёт у семи богатырей. Блуждая по лесу, царевна набрела на их терем. К ней бросился пёс, который залаял, но тут же стал играть и ластиться.
Свою собачью преданность он проявляет, пытаясь уберечь царевну от отравленного яблока, брошенного Чернавкой. Соколка “жалко смотрит, грозно воет”.
Оставив собаку за дверью, царевна проглотила кусочек яблока и умерла. Пришедшим богатырям пёс смог сообщить о беде только ценой своей жизни. Он проглотил ядовитое яблоко и погиб.
Подробнее: https://obrazovaka.ru/question/pes-iz-skazki-o-mertvoj-carevne-sem-bogatyrej-i-mertvaya-carevna-69125
Объяснение:
э
это ответ на твой пример