№1.
Объяснение:
Пусть сторона 1-го квадрата равна А, а сторона 2-го равна В. Тогда можно составить систему уравнений:
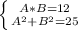
Выражаем значение одной из переменных из 1-го уравнения и подставляем во 2-е:
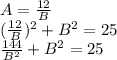
Домножим все слагаемые на B^2, и затем заменим B^2 на t:
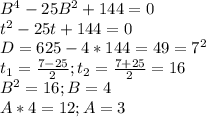
Значение t1 меньше 0, что не соответствует здравому смыслу, поэтому его не рассматриваем.
ответ: 3 и 4 см
-----------------
№2.
Объяснение:
Пусть один катет равен a, второй равен b. Тогда, исходя из теоремы Пифагора, составим систему уравнений:
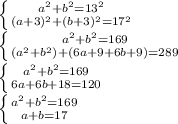
Выразим одну из переменных из 2-го уравнения и подставим в 1-е:
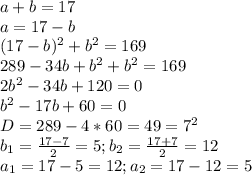
Таким образом, катеты равны 5 и 12 см. Площадь такого треугольника будет равна 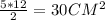
ответ: 30 см^2
a) На пять делятся числа вида 5n, n ∈ N.
Чисел от M до N, которые делятся на d будет:![[\frac{N}d] - [\frac{M}d]](/tpl/images/0158/8037/03187.png) ([x] - целая часть)
([x] - целая часть)
Чисел от M до N, которые не делятся на d будет:
c) Чисел от M до N, которые делятся или на d1 или на d2 будет:![( [\frac{N}{d1}] - [\frac{M}{d1}]) + ( [\frac{N}{d2}] - [\frac{M}{d2}]) - ( [\frac{N(d1,d2)}{d1d2}] - [\frac{M(d1,d2)}{d1d2}])](/tpl/images/0158/8037/13c66.png)
((d1,d2) - НОД)
d) p(не делится на двадцать девять) = 1 - p(делится на двадцать девять)