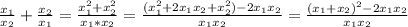
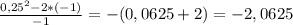
ответ:k=7 при котором параллельные никогда не пересекутся.
Вначале строим график: х-по оси абсцисс, у-ординат.
строим график функции у=7х-8( т.к. это прямая то по двум точкам например если х берем 0,подставляя это значение в функцию
у=7*0-8
у =-8 откладываем на графике
другое значение х берем 2, тогда аналогично у= 6.Откладываем н графике .Через 2 точки ((0;-8) и (2;6))чертим прямую.
Рассматриваем вторую функцию у=кх+6
предположим что х=0, тогда у= 6 Откладываем на графике точку (0;6).Видим, что в первой функции у=7х-8 точка (2;6) соответствует точка во второй функции (0;6) ( т.е. сдвинута влево по оси абсцисс на 2). Проводим линию, параллельную 1-ой функции и выбираем на прямой любую точку. Например (-2;-8)
т.е. х=-2 у=-8
подставляем в уравнение у=кх+6
-8 = к*(-2) + 6
k=7
Пусть координаты искомой точки М (0,у, 0). Тогда
|MA|=|MB|
√(1+(y-2)²+9)=√(1+(y+3)²+16)
(y-2)²=(y+3)²+7 => y²-4y+4=y²+6y+9+7
-10y=12 => y=-1.2.
М (0:-1,2;0).