Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть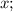 
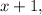
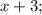
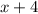- пять последовательных натуральных чисел, тогда их сумма равна:
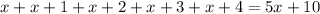
Очевидно, что каждое слагаемое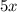 
и 
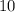делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть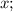 
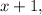
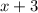- четыре последовательных натуральных числа, тогда их сумма равна:
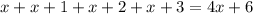
Очевидно, что первое слагаемое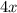 
делится на 4, а второе слагаемое 
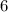не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть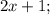 
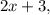
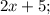
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
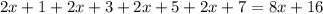
Очевидно, что каждое слагаемое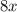 
и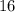 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть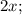 
; 
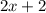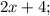
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
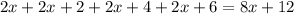
Очевидно, что каждое слагаемое 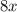и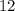 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.
1. Нули:
х=0, тогда у=2
4-|х+2|=0
|х+2|=4
Это равносильно двум уравнениям:
х+2=4
х+2=-4
или
x=2
x=-6
2. Промежутки знакопостоянства:
4-|х+2|>0
или
|х+2|<4
или
-4<х+2<4
-6<х<2
Функция положительна на интервале (-6;2) и соответственно отрицательна при остальных значениях х.
3. Функция равносильна двум.
у=4-х-2=2-х (при х+2>0 или х>-2)
у=4+х+2=6+х (при х+2<0 или х<-2)
Их производные соответственно равны -1 и 1
Следовательно первая убывает (на промежутке от -2 до + бесконечности), а вторая возрастает (от - бесконечности до -2)
(х-2)-(3х-1)=2х(х-4)+2
х-2-3х+1=2х²-8х+2
х-2-3х+1-2х²+8х-2=0
-2х²+6х-3=0
а=-2 (старший коэффициенты)
b=6 (2ой коэффициент)
c=-3 (свободный член )