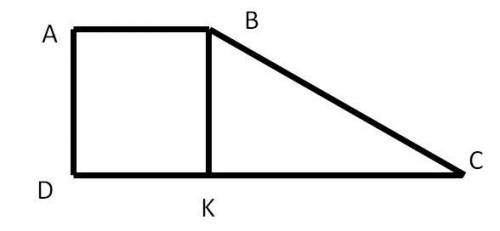
Пусть АВСD - данная трапеция, AB || CD; AB = AD;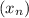 
- арифметическая прогрессия.
Пусть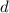 
- разность прогрессии, AB = 
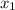По формуле 
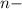ого члена имеем: BC = 
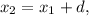CD =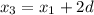 
Периметр трапеции равен: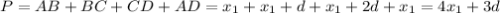 
, т.е.
.
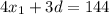Опустим высоту BK = AD = 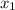⇒ ABKD - квадрат ⇒ KD = 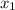⇒ CK = CD - KD = 
=
.
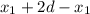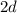В ΔВКС (∠К = 90°) по теореме Пифагора: ВС² = ВК² + СК² =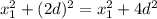 
⇒ 
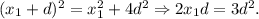
Имеем систему:
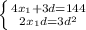
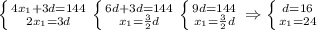
Тогда AD = AB = 24 дм, BC = 24 + 16 = 40 дм, CD = 24 + 2 · 16 = 56 дм.
ОТВЕТ: 24 дм; 24 дм; 40 дм; 56 дм.
Доп. вопросы:
1. d = 16
2. Теорема Пифагора
3. Неравенство треугольника: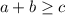 
4. Сторона основания (CD).
Это задача на размещение без повторений, т.е. при данном размещении 1 человек не может в одной и той же комбинации занять 2 места сразу.
(То, что Вы написали P₄=4! - в размещении используется только тогда, когда число размещений равно числу объектов - формула А₄⁴=P₄=4!), фоа здесь используем формулу размещения:
А³₄=4!/(4-3)!=4!/1!=4*3*2=24
4*3*2 - означает, что в каждой комбинации 1-ый человек может выбрать любое из 4-х мест,
2-ой - любое из 3-х оставшихся,
3-й - любое из 2-х оставшихся