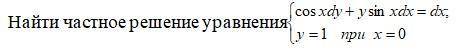
15.
А1. √52=√(4×13)=2√13
ответ: 1
А2. х²-4х=0
Сумма корней равна коэффициенту перед х умноженному на -1.
ответ: 4
А3. х²-9=0
Произведения корней равно свободному члену.
ответ: 4
А4. х²=16
х1=4
х2=-4
4-(-4)=8
ответ: 1
А5. Третье уравнение это сумма двух неотрицательной величины и положительной величины. Она не может равняться нулю.
ответ: 3
В1. √(25х²у^5)=5ху²√у
В2. Выражение имеет смысл, следовательно а≤0
При внесении отрицательного числа под корень, за корнем остаётся минус
а√(-а)=-√(-а³)
С1. (a+b)×2/|(a+b)|=-2
ответ: -2
Если будут вопросы – обращайтесь :)
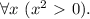
![! \left[ \forall x \ (x^2\ \textgreater \ 0)\right] \Leftrightarrow \exists x \ (x^2 \leq 0).](/tpl/images/0564/9047/dadb8.png)
извини