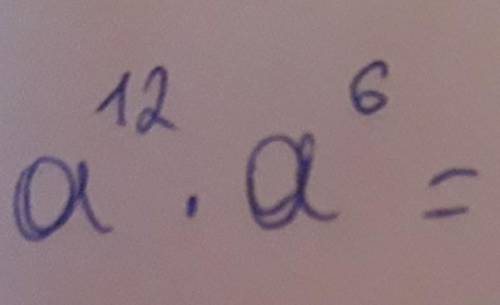
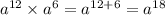
a12×a6= a12+6=a18 ( числа - это степени)
2)D=36+160=196
x1=(6+14)/2=10; x2=(6-14)/2=-4
cosx+sinx=0
умножу все на √2/2
√2/2*cosx+√2/2*sinx=0
sin(pi/4+x)=0
pi/4+x=pin
x=-pi/4+pin (n∈Z)
лишние корни могут появиться только в левом трехчлене, они могут нарушить ОДЗ подкоренного выражения, которое должно быть неотрицательным. Подставлю их и проверю это...
x1=10, вспомним. что pi=3.14, значит 10=3pi+0.58 примерно, это четвертая координатная четверть, там и синус и косинус отрицательные, значит подкоренное выражение отрицательно, что недопустимо. Поэтому x1=10 не подходит
x2=-4=-pi-0.86-вторая координатная четверть. там синус положителен, косинус отрицателен . Причем . суды по значению , х2 находится в интервале между pi/2 и pi/2+pi/4-где значение синуса превосходит по модулю значение косинуса. поэтому подкоренное выражение будет положительно.
ответ x={-4; -pi/4+pn;n∈Z}
пусть а - сторона основания, а l - апофема, тогда формула площади поверхности конуса равна 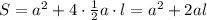
Подставим вместо а и S их значения и найдем апофему l
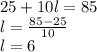
Через апофему проведем сечение пирамиды. В сечении получаем равнобедренный треугольник, основание которого равно стороне а=5, а боковые стороны апофеме l=6. Угол между боковой стороной треугольника и его основанием и есть угол наклона боковой грани пирамиды к плоскости основания. Найдем его, проведем высоту в равнобедренном треугольнике к его основанию. Высота равнобедренного треугольника, проведенная к основанию является так же его биссектрисо и медианой. Поэтому она делит равнобедренный треугольник на два равных прямоугольных треугольника. Найдем косинус искомого угла из прямоугольного треугольника.
Cos A=2,5/6=25/60=5/12 Отсюда следует, что угол наклона боковой грани к плоскости основания пирамиды равен arccos (5/12)