task/29635004 Найди наибольший отрицательный корень уравнения sin²x - 5sinx*cosx + 2 = 0
sin²x - 5sinx*cosx + 2 = 0 ⇔sin²x - 5sinx*cosx + 2(sin²x+cos²x) = 0 ⇔
3sin²x - 5sinx*cosx +2cos²x = 0 || : cos²x ≠ 0 || ⇔3tg²x -5tgx +2 =0 ⇔
[ tgx = 1 ; tgx =2/3 . ⇔ [ x = π/4 +πn ; x =arctg(2/3) + πn , n∈ℤ .
Корни отрицательные при n ≤ -1. Между максимальными отрицательными корнями имеет место неравенство: arctg(2/3) - π < π/4 - π < 0 . * * * arctg(2/3) < arctg1 = π/4 * * *
ответ : - 3π/4.
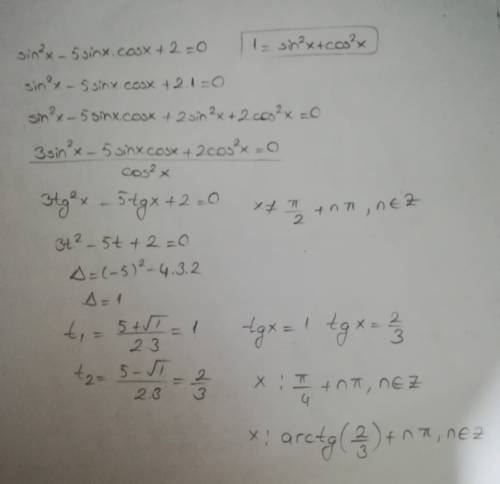
1) 3x-50
2) 2x^2-2x
Объяснение:
1) 5(x-8)-2(5+x)=5x-40-10-2x=3x-50
1. Здесь умножаем число на каждый одночлен в скобках
2. Получаем:
1) 5*x=5x
2) 5*(-8)=-40
3) (-2)*5=-10
4) (-2)*x=-2x
3. Складываем получившиеся одночлены: 5x+(-40)+(-10)+(-2x)=5x-40-10-2x
4. Приводим подобные слагаемые и получаем ответ: 5x-40-10-2x=5x-2x+(-40-10)=3x-50
2) x(x^2+x-2)-x^2(x-1)=x^3+x^2-2x-x^3+x^2=2x^2-2x
См. алгоритм 1
1) x*x^2=x^3 (степени складываются)
2) x*x=x^2 (см. 1)
3) x*(-2)=-2x
4) -x^2*x=-x^3
5) -x^2*(-1)=x^2
x^3-x^3+x^2+x^2-2x=2x^2-2x