ответ: y'=2*x+4.
Объяснение:
Так как областью определения данной функции является вся числовая ось, то зафиксируем некоторую (любую) точку x0 и придадим аргументу x приращение Δx. По определению производной, y'(x0)=lim [y(x0+Δx)-y(x0)]/Δx при Δx⇒0. В нашем случае y(x0)=x0²+4*x0, y(x0+Δx)=(x0+Δx)²+4*(x0+Δx)=x0²+2*x0*Δx+(Δx)²+4*x0+4*Δx, откуда y(x0+Δx)-y(x0)=2*x0*Δx+(Δx)²+4*Δx. Разделив это выражение на Δx, находим [y(x0+Δx)-y(x0)]/Δx=2*x0+Δx+4. Предел это выражения при Δx⇒0, очевидно, равен 2*x0+4, так что y'(x0)=2*x0+4. Но так как x0 - любая точка из области определения, то, заменяя x0 на x, получаем y'(x)=2*x+4.
Объяснение:
Чтобы произвести вычитание алгебраических дробей, надо знаменатели этих дробей разложить на множители.
В знаменателе первой дроби можно вынести за скобку x. В знаменателе второй дроби применяем формулу разности квадратов.
Получаем преобразованную дробь:
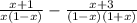
Ну а теперь приведем дроби к общему знаменателю:
Числитель и знаменатель первой дроби можно домножить на (1 + x), то есть, мы ищем, каких слагаемых нет у двоих дробей и на эти слагаемые домножаем числитель и знаменатель.
Получаем следующую картину:
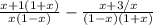
Теперь раскроем скобки. Получим:
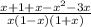
Приведем подобные слагаемые и получим:
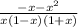
Задача решена.
x=11:2
Объяснение:
16x^2-(4x-2)(4x+3)=-22
9x^2-(3y-1)(3y-2)=-16
x=11:2
(4x+1)(4x-3)+(2x-10)(8x+1)
(8x+1)(2x-10)-(4x-3)(4x-1)
x=-0,157654