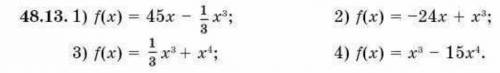
1) Прямая пропорциональность у=кх, подставим значения х и у заданной точки -5=к*3, отсюда к=-5/3=-1 2/3, и функция у=-1 2/3*х
2) В точке пересечения с осью координата другой оси =0
а) с оью 0х у=0, тогда 0=1.2х-24, 1.2х=24, х=20; с осью 0у х=0, у=-24
б) 0х: у=0, 0=-3/5х+2, х=10/3=3 1/3; ось 0у х=0, у=2
в) график у=10 не зависит от х, т.е. для любого х прямая параллельна 0х и ее не пересекает, а пересекает только у=10
3) раз график параллелен оси 0х, то функция не зависит от х (см. пример 2), и имеет вид у=в, для заданной точки М(-3;1) у=1, значит в=1 и функция имеет вид у=1 для любого х, в том числе х=-3
- + -
_____- 3√5______ 3√5 _____
min max
x = - 3√5 - точка минимума, так как при переходе через эту точку призводная меняет знак с "-" на "+" .
x = 3√5 - точка максимума, так как при переходе через эту точку призводная меняет знак с "+" на "-" .
2) f(x) = - 24x + x³
f'(x) = - 24(x)' + (x³)' = - 24 + 3x²
f'(x) = 0 ⇒ - 24 + 3x² = 0
x² = 8
x₁,₂ = ± √8 = ± 2√2
+ - +
______ - 2√2 ______ 2√2 ______
max min
- + +
______ - 0,25 ____________0_____
min точка перегиба
4) f(x) = x³ - 15x⁴
f'(x) = (x³)' - 15(x⁴)'= 3x² - 15 * 4x³ = 3x² - 60x³ = 3x²(1 - 20x)
f'(x) = 0
3x² (1 - 20x) = 0
x₁ = 0
x₂ = 0,05
+ + -
______ 0,05 _______ 0 ______
точка перегиба max