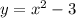- квадратичная функция, график - парабола, получается путём параллельного переноса по оси ОУ вниз на 3 ед. Вершина (0;-3), ветви направлены вверх, так как a>0.
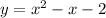- квадратичная функция, график - парабола, ветви направлены вверх(a>0), найдём координаты вершины: 
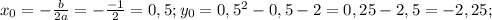(0,5;-2,25), можем ещё найти точки пересечения с осями при х=0 y=-2, y=0, тогда решим квадратное уравнение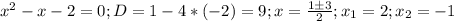 
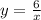- функция обратной пропорциональности, график - гипербола. Здесь с модулем чуть по-другому. Хотя, можно, конечно, сказать, что 
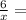I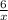
I, тогда преобразования те же самые, но здесь ещё возможен такой вариант: под модулем находится только аргумент, поэтому та часть графика, которая находится левее оси ОУ, удаляется, а что правее - симметрично отображается по оси OY. Всё, что на координатных плоскостях отображается красным - подлежит удалению, эта часть симметрично отображается. Чёрным на графике обозначен конечный график со всеми преобразованиями.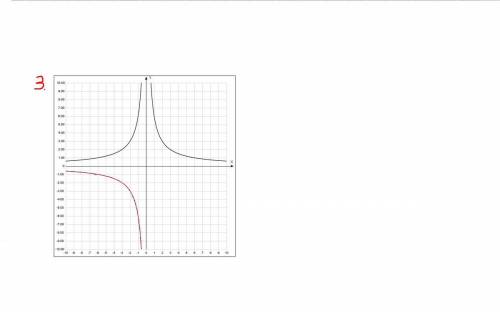 
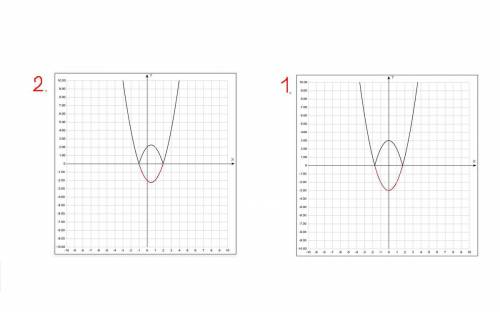
№2
у=х-(-3)
3х-3у=-9
3х-3(х+3)=-9
3х-3х=-9+9
0=0 следовательно прямые совпадают и имеют бесконечное множество решений
№3
х-у=3
2х-у=7
-2х+2у=-6
2х-у=7
-2х+2у+2х-у=-6+7
у=1
х=3+у
х=4
следующий пример
х-2у=1
2х+4у=18
-2х+4у=-2
2х+4у=18
-2х+4у=2х+4у=-2+18
8у=16
у=2
х=2у+1
х=5
№4
1 этап. Составление матем. модели
х - количество 5-ти рублёвых монет
у - клоичество 1-но рублёвых монет
составим систему
х+у=200
5х+у=800
2 этап. Работа с составленной мат. моделью
х+у=200
5х+у=800
будем решать методом подстановки
у=200-х
5х+у=800
5х+200-х=800
4х=600
х=150
у=200-150=50
3 этап ответ на поставленный вопрос
ответ: 150 пятирублёвых монет и 50 рублёвых монет