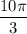В левой части можно применить формулу косинуса двойного угла:
В правой части можно заменить по формуле приведения:
Тогда уравнение будет выглядеть так:
Используем формулу суммы косинусов:
В нашем случае получается:
Так как , то:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Значит, имеем два варианта:
Теперь подбираем корни, которые принадлежат отрезку . Для этого можно решить двойное неравенство для каждой серии корней.
Для первой серии:
Не забываем, что - это обязательно целое число. В данном промежутке есть только одно такое: 2. Значит, . Подставляем это значение в серию корней, для которой мы решали неравенство.
Одно искомое уже нашли. Теперь тем же самым образом проверим вторую серию корней.
Опять же, учитывая то, что - целое число, данное неравенство НЕ ИМЕЕТ РЕШЕНИЙ, поскольку в получившемся промежутке нет целых чисел.
Итого мы нашли одно значение, которое одновременно и является корнем уравнения, и входит в промежуток , а именно .
1)sinА^2+cosA^2= 1 Тогда cos(A) =√ 1-sinA^2= √1( 2/7)^2=√1-4/49=√45/49=√45/7=√9*√5/7=3√5/7 Вычислим тангенс, зная, что тангенсом острого угла называется отношение синуса угла к его косинусу. tg (A) =2/7 : 3√5/7=2*7/3√5*7=2/3√5 ctgA=cosa/sina=3√5/7/2/7=3√5/2 2)a) (sina+cos)^2+(sina-cosa)^2= =sin^2a+2sinacosa+cos^a+sin^2a-2sinacosa+cosa= =2sin^2a+2cos^2a=2 б) cos²α- cos⁴α+sin⁴α=cos²α(1- cos²α)+sin⁴α=cos²α·sin²α+sin⁴α
( sin²α=1-cos²α)
=sin²α(cos²α+sin²α)=
(sin²α+cos²α= 1)
=sin²α В) 1-cos^2a/1-sin^2a=sin^2a/cos^2a=tga 3)sin>0 cos<0 tg,ctg<0 750=2*360+30-1 2 полных оборота и поворот на 30 градусов 1 четверть в ней sin,cos,tg,ctg>0
В левой части можно применить формулу косинуса двойного угла:
В правой части можно заменить по формуле приведения:
Тогда уравнение будет выглядеть так:
Используем формулу суммы косинусов:
В нашем случае получается:
Так как , то:
, то:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Значит, имеем два варианта:
Теперь подбираем корни, которые принадлежат отрезку![\boldsymbol{\left[3\pi;\ \dfrac{9\pi}{2}\right]}](/tpl/images/4756/3407/76927.png) . Для этого можно решить двойное неравенство для каждой серии корней.
. Для этого можно решить двойное неравенство для каждой серии корней.
Для первой серии:
Не забываем, что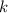 - это обязательно целое число. В данном промежутке есть только одно такое: 2. Значит,
- это обязательно целое число. В данном промежутке есть только одно такое: 2. Значит,  . Подставляем это значение в серию корней, для которой мы решали неравенство.
. Подставляем это значение в серию корней, для которой мы решали неравенство.
Одно искомое уже нашли. Теперь тем же самым образом проверим вторую серию корней.
Опять же, учитывая то, что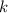 - целое число, данное неравенство НЕ ИМЕЕТ РЕШЕНИЙ, поскольку в получившемся промежутке нет целых чисел.
- целое число, данное неравенство НЕ ИМЕЕТ РЕШЕНИЙ, поскольку в получившемся промежутке нет целых чисел.
Итого мы нашли одно значение, которое одновременно и является корнем уравнения, и входит в промежуток![\left[3\pi;\ \dfrac{9\pi}{2}\right]](/tpl/images/4756/3407/d29f6.png) , а именно
, а именно  .
.
ответ: