Решать задание по Локальной теореме Лапласа: 1. В каждом из 700 независимых испытаний событие A происходит с постоянной вероятностью 0,35. Найдите вероятность того, что событие A происходит: а) ровно 270 раз; б) меньше чем 270 и больше чем 230 раз; в) больше чем 270 раз.
2. При установившемся технологическом процессе на ткацкой фабрике происходит 10 обрывов нити на 100 веретен в час. Определите: а) вероятность того, что в течение часа на 80 веретенах произойдет 7 обрывов нити; б) наивероятнейшее число обрывов нити на 80 веретенах в течение часа.
3. Вероятность того, что деталь первого сорта равна 0.4. Сделано 150 деталей. Найти вероятность того, что среди них 68 деталей первого сорта.
4. Вероятность появления события в каждом из независимых испытаний равна p.
Найти вероятность того, что событие состоится n раз, если проведения m испытаний.
ответ представить с точностью до трех значащих цифр.
р=0.75, n=87, m=120
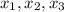

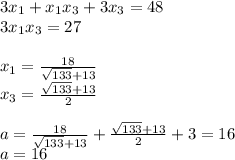
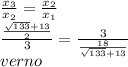
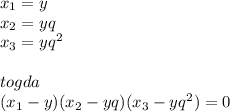
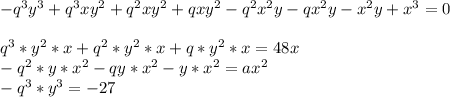
Объяснение:
1.Так как количество опытов n = 700 довольно велико, то используем формулы Лапласа.
а) Задано: n = 700, p = 0,35, k = 270.
Найдем P700(270). Используем локальную теорему Лапласа.
Находим:
Значение функции φ(x) найдем из таблицы:
б) Задано: n = 700, p = 0,35, a = 230, b = 270.
Найдем P700(230 < k < 270).
Используем интегральную теорему Лапласа (23), (24). Находим:
Значение функции Ф(x) найдем из таблицы:
в) Задано: n = 700, p = 0,35, a = 270, b = 700.
Найдем P700(k > 270).
2.Статистическая вероятность обрыва нити в течение часа равна p = 10/100 = 0,1 и, следовательно, q = 1 – 0,1 = 0,9; n = 80; k = 7.
Поскольку n велико, то используется локальная теорема Лапласа (23). Вычисляем:
Воспользуемся свойством φ(-x) = φ(x), находим φ(0,37) ≈ 0,3726, а затем вычисляем искомую вероятность:
Таким образом, вероятность того, что в течение часа на 80 веретенах произойдет 7 обрывов нити, приближенно равна 0,139.
Наивероятнейшее число k0 наступлений события при повторных испытаниях определим по формуле (14). Находим: 7,1 < k0 < 8,1. Поскольку k0 может быть только целым числом, то k0 = 8.