Решаем пропорцией
Перемножаем крест накрест:
(7-2)(3х+1)=80х-30
-65х=-35
х=7/13
Исходя из отношения сторон 2:19, пусть ширина будет равна 2х, а длина - 19х. Мы знаем, что площадь находится по формуле: S=a*b. Тогда мы можем составить уравнение, подставив наши переменные, 2х*19х=152 или 38х^2=152 (во второй степени)
Узнаём чему равен х.
38х^2=152 => х^2=4 => х=√4=2 (т.к. в данном случае не может быть отрицательного корня)
Теперь узнаём чему равны стороны прямоугольника.
Ширина=2х=2*2=4
Длина=19х=19*2=18
И теперь с формулы нахождения периметра Р=(a+b)*2 мы можем найти периметр.
Р=(18+4)*2=88
Как-то так.
.
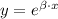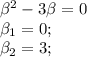
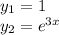
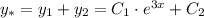
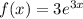
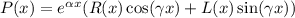, где R(x) и S(x) - полиномы, которое имеет частное решение.
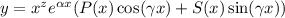, где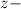 
кратность корня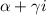 
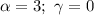
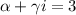является корнем характеристического уравнения кратности z=1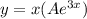
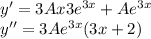
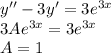
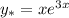
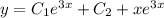
(8х-3):5=(3х+1):10 умножаем на 10 обе стороны получается
2*(8х-3)=(3х+1)
16х-6=3х+1
16х-3х=1+6
13х=7
х= 13:7-ых(дробью)