и 
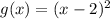. Область определения функции есть промежуток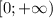 
, т.к. выражение имеет смысл только при неотрицательных значениях. Область значений функции является промежуток 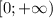. Точки построения графика: (0;0), (1;1), (4;2), (9;3).
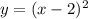является парабола, ветви направлены вверх (т.к. коэффициент при x² : а=1>0). (2;0) - координаты вершины параболы.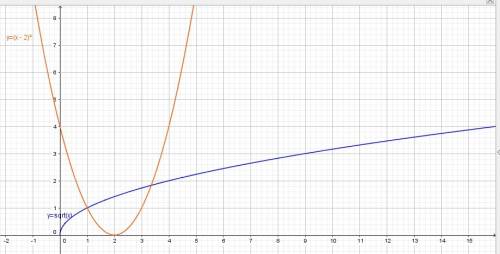
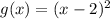и . Область определения функции есть промежуток 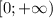, т.к. выражение имеет смысл только при неотрицательных значениях. Область значений функции является промежуток 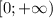. Точки построения графика: (0;0), (1;1), (4;2), (9;3). 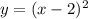является парабола, ветви направлены вверх (т.к. коэффициент при x² : а=1>0). (2;0) - координаты вершины параболы.
вот держи, надеюсь все понятно