
.
Объяснение:
Пара может состоять или из юноши и девушки, или из двух девушек.
Возьмем первого любого юношу. Это 4 варианта.
К нему в пару можно поставить любую из 12 девушек. Это 12 вариантов.
Всего 4*12 = 48 вариантов выбрать первую пару.
Возьмем второго юношу. Это 3 варианта.
К нему в пару можно поставить любую из 11 оставшихся девушек. Это 11 вариантов. Всего 3*11 = 33 варианта.
Возьмем третьего юношу. Это 2 варианта.
К нему в пару можно поставить любую из 10 оставшихся девушек. Это 10 вариантов. Всего 2*10 = 20 вариантов.
Возьмем четвертого юношу. Это 1 вариант.
К нему в пару можно поставить любую из 9 оставшихся девушек.
Это 9 вариантов.
Получилось 9*20*33*48 = 285120 вариантов распределить 4 юношей и 4 девушек по парам.
Еще остается 8 девушек, которых надо тоже распределить на 4 пары.
Отобрать одну пару из 8 человек можно .
Отобрать одну пару из 6 человек можно .
Отобрать одну пару из 4 человек можно .
И четвертая пара образуется сама собой.
Всего .
В итоге получается .
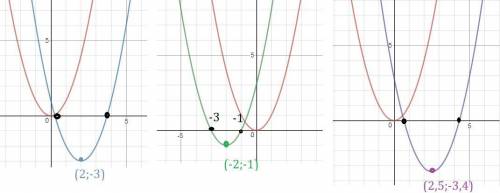
1) Шаблон y=x²
Вершина в точке (2;-3)
Нули функции
(x-2)²-3=0 ⇒
(x-2)²=3
x-2= -√3 или х-2=√3
х=2-√3 или х=2+√3
2) Шаблон y=x²
Вершина в точке (-2;-1)
Нули функции
(x+2)²-1=0 ⇒
(x+2)²=1
x+2= -1 или х+2=1
х=-3 или х=-1
3) Шаблон y=x²
Вершина в точке (2,5;-3,4)
Нули функции
(x-2,5)²-3,4=0 ⇒
(x-2,5)²=3,4
x-2,5= -√3,4 или x-2,5=√3,4
х= 2,5 -√3,4 или х=2,5 +√3,4
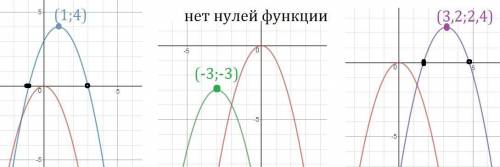
4)Шаблон y= - x²
Вершина в точке (1;4)
Нули функции
-(x-1)²+4=0 ⇒
(x-1)²=4
x-1= -2 или x-1=2
х= -1 или х=3
5)Шаблон y= - x²
Вершина в точке (-3;-3)
Нули функции
-(x+3)²-3=0 ⇒
(x+3)²=-3
уравнение не имеет корней.
Парабола не пересекает ось Ох
6)Шаблон y= - x²
Вершина в точке (3,2;2,4)
Нули функции
-(x-3,2)²+2,4=0 ⇒
(x-3,2)²=2,4
x-3,2= - √2,4 или x-3,2= √2,4
x= 3,2 - √2,4 или x = 3,2+ √2,4
а) 3a²b*b⁴a⁴
3a²+⁴b¹*b⁴
3a^6b¹+⁴
3a^6 b^5
б) (-0.2х²)³*5х²
-0.2х³*х^6*5х²
-1/25*^8 (минус одна целая двадцать пять десятых)