Участник Знаний
1.~ a)~ (x+4)^2=x^2+8x+16\\ b)~ (y-5x)^2=y^2-10xy+25y^2\\ c)~ (3a-2)(3a+2)=(3a)^2-2^2=9a^2-4\\ d)~ (c-2b)(c+2b)=c^2-(2b)^2=c^2-4b^2
2. Разложить на множители:
a)~ x^2-81=x^2-9^2=(x-9)(x+9)\\ b)~ y^2-4y+4=(y-2)^2
в пункте б) опечатка, так что предположил как должно быть
c)~ 36x^4y^2-169c^2=(6x^2y)^2-(13c)^2=(6x^2y-13c)(6x^2y+13c)\\ d)~ (x+1)^2-(x-1)^2=(x+1-x+1)(x+1+x-1)=2\cdot 2x=4x
3. Упростить выражение:
(c+6)^2-c(c+12)=c^2+12c+36-c^2-12c=36
4. Решите уравнение:
a)~ (x+7)^2-(x-4)(x+4)=65\\ x^2+14x+49-x^2+16=65\\ 14x=0\\ x=0
b)~ 49y^2-64=0\\ y^2=\dfrac{64}{49}~~\Rightarrow~~~ y_{1,2}=\pm\dfrac{8}{7}
5. Выполнить действия:
a)~ (4a^2+b^2)(2a-b)(2a+b)=(4a^2+b^2)(4a^2-b^2)=16a^4-b^4\\ b)~ (b^2c^3-2a^2)(b^2c^3+2a^2)=(b^2c^3)^2-(2a^2)^2=b^4c^6-4a^4
6*.Докажите неравенство:
4x^2+9y^2>12xy-0.1\\ 4x^2-12xy+9y^2>-0.1\\ (2x-3y)^2>-0.1
Что и требовалось доказать
Объяснение:
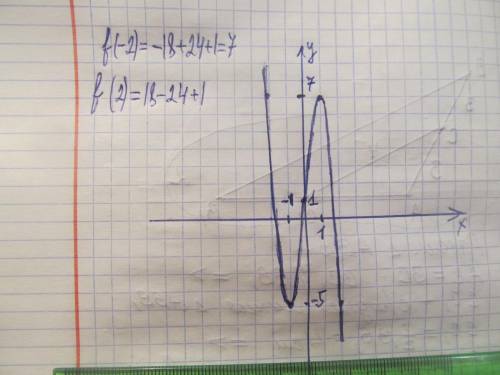
f(x)=-3x³+9x+1
f'(x)=-9x²+9=0 парабола ветвями вниз
x²-1=0; (x-1)(x+1)=0; критические точки х=1; х=-1
---------[-1]----------------------------[1]------------------>x
- + -
f(x) убывает min возрастает max убывает
f(-1)=-9+3+1=-5
f(0)=1
f(1)=9-3+1=7
f(-2)=7;
f(2)=-5
ф-ция убывает при х∈(-∞; -1) U (1; ∞)
ф-ция возрастает при х∈(-1; 1)
при х=-1 значение ф-ции минимально = -5
при х=1 максимально = 7
область определения (-∞; ∞)
область значений (-∞; ∞)
ф-ция общего вида.
(2X-5)^2-36=0
4x²-20x+25-63=0
4x²-20x-11=0
D = (-20)²-4*4*(-11)=400+176=576=24²
x₁ = (20-24)/8 = -1/2= -0.5
x₂ = (20+24)/8 = 44/8 = 5.5