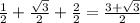Пусть катеты a и bа/b=3/4a=3b/4пусть меньший отрезок, на которые делит высота гипотенузу равен x тогда второая x+14по теореме высота h^2=x(x+14)по теореме пифагора a^2=x^2+h^2=x^2+x(x+14)=2x^2+14xснова по теореме пифагора: b^2=h^2+(x+14)^2=x(x+14)+(x+14)^2=x^2+14x+x^2+28x+196=2x^2+42x+196но так как мы сказали что a=3b/4 => a^2=9b^2/16=9(2x^2+42x+196)/169(2x^2+42x+196)/16=2x^2+14x9(2x^2+42x+196)=32x^2+224x18x^2+378x+1764=32x^2+224x-14x^2+154x+1764=014x^2-154x-1764=0x^2-11x-126=0x=18 осталось найти a и b и найти площадь
Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов: Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.
Объяснение:
sinα+sin2α+sin3α = sin 30° + sin (2 * 30°) + sin (2 * 30°) =
= sin 30° + sin 60° + sin 90° =