у/5.
Объяснение:
Упростите выражение:
(x+4)/(x-3) * (3x-9)/(x²+8x+16) : 15/(xy+4y)=
1)(x+4)/(x-3) * (3x-9)/(x²+8x+16)=
В числителе второй дроби вынести 3 за скобки, в знаменателе второй дроби квадрат суммы, свернуть:
=(x+4)/(x-3) * [3(x-3)]/(x+4)²=
Чтобы умножить дробь на дробь, нужно числитель первой дроби умножить на числитель второй, а знаменатель первой дроби умножить на знаменатель второй:
=[(x+4)*3(x-3)] / [(x-3)*(x+4)(x+4)]=
сокращение (x+4) и (x+4) на (x+4), (x-3) и (x-3) на (x-3):
=3/(x+4);
2)3/(x+4) : 15/(xy+4y)=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
=[3*у(x+4)] / [(x+4)*15]=
сокращение (x+4) и (x+4) на (x+4), 3 и 15 на 3:
=у/5.
Сначала мы пишем систему и смотрим на коэффициенты при х и у.
В данном случае, особой разницы нет, поэтому останавливаемся на коэффициентах при х. В первом уравнении коэффициент при х равен 4, а во втором 3. Нам надо, чтобы при почленном сложении двух уравнений сумма коэффициентов при х равнялась нулю. Этого можно добиться искусственно, если первое уравнение домножить на 3, а второе уравнение домножить на (-4) (данная операция обозначена вертикальными "палочками", после которых стоит знак умножения на нужное нам число
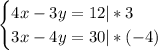
Получаем следующую систему:
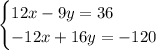
Теперь складываем уравнения "почленно", т.е. иксы с иксами, игреки с игреками, свободные члены со свободными членами. В результате получаем:
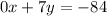
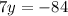
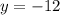
Осталось найти х. Для этого найденное значение у=-12 подставим в любое из первоначальных уравнений, например, в первое:
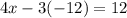

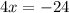

Осталось записать ответ. Допускаются следующие записи:
х=-6, у=-12 или (-6;-12)
х ---скорость из А в В
за 5 часов со скоростью х мотоциклист проехал путь = 5*х км
обратно 48 км со скоростью х он ехал (48/х) часов
оставшуюся часть пути (5х-48) км со скоростью (х+4) он ехал
(5х-48)/(х+4) часов
на обратный путь затрачено на 15 мин меньше, 15 мин = 15/60 часа = 1/4 часа
5 - (48/x + (5х-48)/(х+4)) = 1/4
(48(x+4) + x(5х-48)) / (x*(х+4)) = 5 - 1/4 = (20-1)/4 = 19/4
4*(48x+48*4 + 5х*x-48x) = 19*(x*x+4x)
х^2 -19*4x + 16*48 = 0
D = 19*19*16 - 4*48*16 = 16*(19*19-4*48) = 16*169 = 4*4*13*13
x1 = (19*4 + 4*13)/2 = 2*(19+13) = 2*32 = 64
x2 = (19*4 - 4*13)/2 = 2*(19-13) = 2*6 = 12
ПРОВЕРКА:
за 5 часов со скоростью 12 км/час мотоциклист проехал путь 5*12 = 60 км
обратно 48 км он с той же скоростью проехал за 48/12 = 4 часа
оставшиеся 60-48 = 12 км он ехал со скоростью 12+4 = 16 км/час
время на оставшуюся часть пути 12/16 = 3/4 часа ---это на 15 мин меньше, чем 5-4=1 час
за 5 часов со скоростью 64 км/час мотоциклист проехал путь 5*64 = 320 км
обратно 48 км он с той же скоростью проехал за 48/64 = 3/4 часа
оставшиеся 320-48 = 272 км он ехал со скоростью 64+4 = 68 км/час
время на оставшуюся часть пути 272/68 = 4 часа
4+3/4 ---это на 15 мин меньше, чем 5 часов
оба ответа возможны (либо мотоциклист ехал медленно ---со скоростью 12 км/час и поэтому проехал меньшее расстояние между А и В, либо он ехал быстро и тогда А и В расположены дальше друг от друга...)
как-то не часто встречается задача на движение с двумя вариантами ответа...