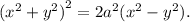
4а-(а+6)=?
Это значит,что то,что в скобках,ты должен оставить без скобок...т.е:
4а-а-6=?
Когда ты раскрываешь скобки,то должен переставить на противоположные знаки перед скобкой,то,что находится у тебя в скобках!
Если перед скобкой стоит +,и с скобках например:(4а+8)
То при раскрывании у тебя получится:
4а+8!
Запомни, минус на минус будет плюс
плюс на плюс будет плюс
минус на плюс будет минус
плюс на минус будет минус
А привести подобные это значит,что все числа с одинаковым буквенным коэффициентом сложить или вычесть..т.е.
4а+а будет 5а
Поэтому в этом выражении 4а-(а+6)=?
4а-а-6 =3а-6
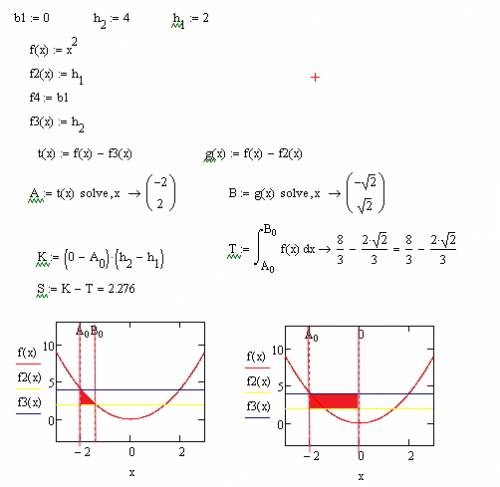
Вычисляем площадь прямоугольника на правом графике (K) площадь прямоугольника равна первой стороне помноженной на вторую
Вычисляем площадь фигуры на первом графике (Это площадь под графиком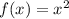 
до графика f2(x)=2
Берём определённый интеграл где за нижний индекс будет выступать меньший корень уравнения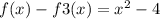 
находим корень меньший он равен -2 пишем в интеграл на нижний индекс -2 Это начало интегрирования (интеграл от 
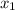до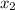 
где начало 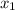а конец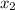
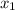мы нашли это -2 (нижний индекс)
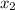это меньший корень уравнения 
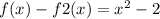он равен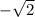 
определили точки интегрирования теперь ставим функцию которую интегрируем f(x) интегрируем по x
Площадь ограниченная графиком = равна площади прямоугольника без площади которую нам даст интеграл .
S=K-T
Описать как брать интеграл вручную не стану есть много литературы в нете и это долго .
Основные функции
\left(a=\operatorname{const} \right)
x^{a}: x^a
модуль x: abs(x)
\sqrt{x}: Sqrt[x]
\sqrt[n]{x}: x^(1/n)
a^{x}: a^x
\log_{a}x: Log[a, x]
\ln x: Log[x]
\cos x: cos[x] или Cos[x]
\sin x: sin[x] или Sin[x]
\operatorname{tg}x: tan[x] или Tan[x]
\operatorname{ctg}x: cot[x] или Cot[x]
\sec x: sec[x] или Sec[x]
\operatorname{cosec} x: csc[x] или Csc[x]
\arccos x: ArcCos[x]
\arcsin x: ArcSin[x]
\operatorname{arctg} x: ArcTan[x]
\operatorname{arcctg} x: ArcCot[x]
\operatorname{arcsec} x: ArcSec[x]
\operatorname{arccosec} x: ArcCsc[x]
\operatorname{ch} x: cosh[x] или Cosh[x]
\operatorname{sh} x: sinh[x] или Sinh[x]
\operatorname{th} x: tanh[x] или Tanh[x]
\operatorname{cth} x: coth[x] или Coth[x]
\operatorname{sech} x: sech[x] или Sech[x]
\operatorname{cosech} x: csch[x] или Csch[е]
\operatorname{areach} x: ArcCosh[x]
\operatorname{areash} x: ArcSinh[x]
\operatorname{areath} x: ArcTanh[x]
\operatorname{areacth} x: ArcCoth[x]
\operatorname{areasech} x: ArcSech[x]
\operatorname{areacosech} x: ArcCsch[x]
[19.67] =19: integral part of (19.67) - выделяет целую часть числа