Найти экстремумы функции y=(1/3)*x^3-2x^2 объясните подробно, как правильно найти производную, и решать далее.

👇

Ответ:

lilia25021

09.10.2020

Производная находится так.
степень которая стоит в X ставится перед ним. тоесть 3*1/3x^2 (а сама степень вычитается на 1)

После чего решаем обычное биквадратное уравнение с вынесением Х. Находим две точки. Дальше определяем знаки. Берём число строго меньше нуля и подставляем его в начальное выражение, считаем и получаем либо положительное либо отрицательное число. После берём чила от 1 до 3-х и делаем тоже самое. А после строго больше четырёх.

Точка максимума - это где знак переходит с - на +
Точка минимума - это где знак переходит с + на -

Найти экстремумы функции y=(1/3)*x^3-2x^2 объясните подробно, как правильно найти производную, и реш

4,8(91 оценок)

Открыть все ответы

Ответ:

anjnazarova

09.10.2020

абсциссf точки х₀ = 1

Объяснение:

Прежде всего найдем уравнение касательной.

Уравнение касательной имеет вид

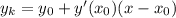
y_k = y_0 + y'(x_0)(x - x_0)

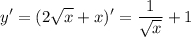
$\displaystyle y'=(2\sqrt{x} +x )'=\frac{1}{\sqrt{x} } +1$

Рассмотрим уравнение касательной в точке х₀ (эту точку нам и надо найти)

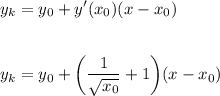
$\displaystyle y_k = y_0 + y'(x_0)(x - x_0)y_k = y_0 + \bigg(\frac{1}{\sqrt{x_0} } +1\bigg)(x - x_0)$

Для того, чтобы две прямые были параллельны, необходимо, чтобы в уравнениях прямых коэффициенты при х были бы равны.

У прямой у = 2х коэффициент при х равен 2

У касательной коэффициент при х равен 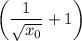$\displaystyle \bigg(\frac{1}{\sqrt{x_0} } +1\bigg)$

Приравняем коэффициенты и найдем х₀

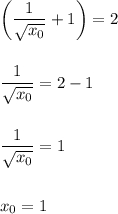
$\displaystyle \bigg(\frac{1}{\sqrt{x_0} } +1\bigg)=2displaystyle \frac{1}{\sqrt{x_0} } =2-1frac{1}{\sqrt{x_0} } =1x_0=1$

Проверим.

Подставим х₀ в формулу касательной.

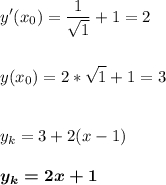$\displaystyle y'( x_0) = \frac{1}{\sqrt{1} } +1=2y(x_0)=2*\sqrt{1} +1 = 3y_k = 3+2(x-1)boldsymbol { y_k = 2x+1}$ - это уравнение касательной в точке х₀=1.

И эта прямая ║ прямой у = 2х

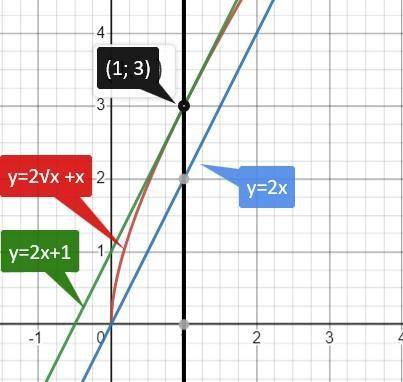
Найти абсциссу точки, в которой касательная к графику функции f(x)=2√x +x параллельна прямой y=2x

4,5(85 оценок)

Ответ:

Adn2001

09.10.2020

Відповідь:

фото.

Пояснення:

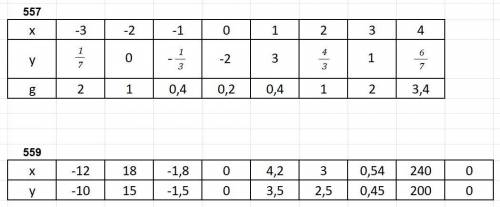
557 номер. Нам дані функції y(x), g(x). В таблиці наведені значення x. Підставляючи кожне значення ікс в функції ми одержуємо відповідні значення y і g. Наприклад, на початку таблиці дано значення x=-3, знайти потрібно y,g. Спочатку x=-3 підставляємо у функцію y(x). Маємо:

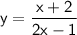
$\displaystyle\mathsf{y=\frac{x+2}{2x-1} }$

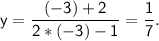
$\displaystyle\mathsf{y=\frac{(-3)+2}{2*(-3)-1}=\frac{1}{7} . }$

Тепер це значення "y" записуємо у таблицю в колонці з x=-3. З знаходженням g аналогічно:

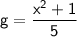
$\displaystyle\mathsf{g=\frac{x^2+1}{5} }$

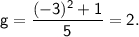
$\displaystyle\mathsf{g=\frac{(-3)^2+1}{5}=2. }$

Це значення "g" записуємо у таблицю в колонці з x=-3.

559 номер. Маємо вихідну функцію і таблицю зі значеннями ікс і ігрик. Якщо коротко - якщо дано значення ікс, а не надо ігрик => підставляємо значення ікс з таблиці у вихідну функцію, і отримуємо значення y. Наприклад, перше значення ікс у таблиці = -12. Отже:

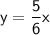
$\displaystyle\mathsf{y=\frac{5}{6} x}$

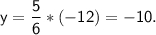
$\displaystyle\mathsf{y=\frac{5}{6} *(-12)=-10.}$

Записуємо це значення ігрик у таблицю в стопчику з x=-12.

Якщо ж нам дано не ікс, а ігрик - все аналогічно. Тільки замість ікса у функцію підставляємо значення ігрик -> виражаємо ікс і знайдене значення заносимо у таблицю. Все.