
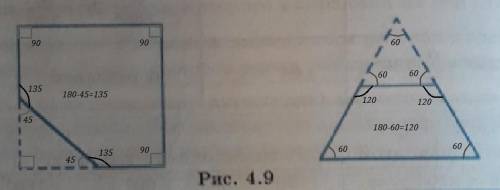
Так как отсечены равнобедренные треугольники (их боковые стороны равны половинам сторон квадрата и правильного треугольника), то углы при основании этих треугольников равны. Для квадрата углы при основании отсеченного треугольника равны по 45°.
Для прав. треугольника получается, что отсекаем не просто равнобедренный треугольник, а равносторонний, т.к. в равнобедренном треугольнике угол при вершине = 60°, а при основании два угла равны по (180°-60°):2=60°.
Из того, что сумма смежных углов = 180° находим оставшиеся углы.
ответ: для пятиугольника углы равны 90° , 90° , 90° , 135° , 135° ; для четырёхугольника углы равны 60° , 120° , 120° , 60° .
Примем вершину пирамиды в начале координат.
Тогда тогда боковые рёбра равны x, y, z.
Выразим площади боковых граней:
xz = 8,
yz = 16,
xy = 18.
Решим эту систему: z = 8/x. y*(8/x) = 16, отсюда у = 2х. Подставим в 3 уравнение: х * 2х = 18, 2х² = 18 или х = +-√9 = +-3.
Отрицательное значение не принимаем, примем х = 3, тогда у =2*3 = 6, z = 8/3.
Найдём стороны основания по Пифагору.
a = √(3² + 6²) = √(9 +36) = √45 = 3√5.
b = √(3² + (8/3)²) = √(6 +(64/9)) = √(100/9) = 10/3.
c =√(6² + (8/3)²) = √(36 +(64/9)) = √(388/9) = √388/3 ≈ 6,566.
Найдём площадь одной из граней.
So = (1/2)xy = (1/2)*3*6 = 9/
ответ: V = (1/3)SoH = (1/3)*9*(8/3) = 8 куб.ед.
.
ну вот,вроде так