Х --столов с одним ящиком ((значит, и ящиков тоже х))) у --столов с двумя ящиками ((ящиков уже 2у)) тогда столов с тремя ящиками будет (х-у) и ящиков в них будет 3*(х-у) столов с четырьмя ящиками будет (14 - х - х) = (14 - 2х) и ящиков в них 4*(14-2х) итого: 33 = х+2у+3х-3у+56-8х 33 = 56-4х-у 4х+у = 56-33 = 23 у = 23 - 4х х и у -- натуральные числа и x>y ---> 4x > 4y -4x < -4y 23-4x < 23-4y у < 23-4y 5y < 23 y < 23/5 ---> y < 4.6 если у = 4 х тогда не получится целым))) если у = 3 х = 5 (и тогда столов с тремя ящиками -- 5-3=2))) если у = 7 х = 4 -- это не возможно, т.к. x > y столов с одним ящиком -- 5, с двумя ящиками 3, с тремя ящиками 2, с четырьмя ящиками 14-5-3-2=4 33 = 5+3*2+2*3+4*4 = 5+6+6+16 = 33))) к сожалению, проще у меня рассуждения не получились)))
1)
Введём замену: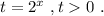
По теореме Виета:
Но так как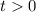 , то -2 не является решением этого уравнения. Выполняем обратную замену:
, то -2 не является решением этого уравнения. Выполняем обратную замену:
ответ: 4.
2)
ответ: -2.
3)
Введём замену: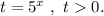
По теореме Виета:
Но так как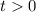 , то -1 не является решением этого уравнения. Выполняем обратную замену:
, то -1 не является решением этого уравнения. Выполняем обратную замену:
ответ: 1.
4)
ответ: 1.
5)
Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:
Продолжаем решение:
Введём замену: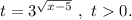
По теореме Виета:
Но так как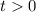 , то -3 не является решением этого уравнения. Выполняем обратную замену:
, то -3 не является решением этого уравнения. Выполняем обратную замену:
ответ: 9.