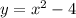
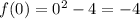
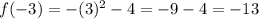
Производная равна угловому коэффициенту касательной к графику функции.
y’ = 2x + b.
Приравняем производную заданным значениям угловых коэффициентов касательных:
2x₁ + b = 6, отсюда b = 6 - 2x₁.
Для другой касательной 2x₂ + b = -5, тогда b = -5 - 2x₂.
Приравняем ординаты параболы и касательной:
6x₁ = x₁2 + bx₁ + c или x₁2 + (b – 6)x₁ + c = 0.
Для другой касательной -5x₂ = x₂2 + bx₂ + c или x₂2 + (b + 5)x₂ + c = 0.
Подставим значение b в каждое уравнение.
x₁² + (6 – 2x₁ – 6)x₁ + c = 0 или x₁² - 2x₁² + c = 0, отсюда с = x₁².
Во второе: x₂² + (-5 – 2x₂ + 5)x₂ + c = 0 или x₂² - 2x₂² + c = 0, отсюда с = x₂².
То есть x₁² = x₂².
Так как по свойству параболы касательные с разными знаками угловых коэффициентов могут быть только к разным веткам параболы, то есть абсциссы точек касания имеют разные знаки.
Тогда x₁ = -x₂.
Подставим эти значения в выражения для b: b = 6 - 2x₁ и b = -5 - 2x₂:
b = 6 - 2x₁ b = 6 - 2x₁
b = -5 – 2(-x₁) b = -5 + 2x₁. Сложив эти уравнения, получаем 2b = 1, откуда b = ½ = 0,5.
Теперь можно определить координаты точек касания из выражения 2x₁ + b = 6.
x₁ = (6 - b)/2 = (6 – 0.5)/2 = 2,75.
Тогда x₂ = -2,75.
Осталось найти коэффициент с.
Его значение определим из выражения 6x₁ = x₁² + bx₁ + c.
с = 6x₁ - x₁² - bx₁ = 6*2,75 – 2,75² – 0,5*2,75 = 7,5625.
ответ: уравнение параболы у = х² + 0,5х + 7,5625.
Подсчитаем количество чисел от 1 до 999999 (число 1 000 000 содержит единицу, его сразу отбросим), в записи которых нет единиц. Каждую цифру можно выбрать любая цифра кроме 1), поэтому все 6 цифр (по правилу произведения) можно выбрать если в числе до значащих цифр стоят нули, мы их просто отбрасываем). При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается.
Получаем всего
6 N = − = 9 1 531440 чисел.
Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.