(3 1/3; 3)
Объяснение:
Система уравнений:
(6-x)²+(-3-y)²=4/9 ·97
(x-2)²+(y-6)²=97/9; 4(x-2)²+4(y-6)²=4·97/9
(6-x)²+(-3-y)²-4(x-2)²-4(y-6)²=4/9 ·97 -4·97/9
(6-x)²-(2x-4)²+(3+y)²-(2y-12)²=0
(6-x-2x+4)(6-x+2x-4)+(3+y-2y+12)(3+y+2y-12)=0
(10-3x)(2+x)+(15-y)(3y-9)=0
10-3x=0; 3x=10; x₁=10/3
2+x=0; x₂=-2
15-y=0; y₁=15
3y-9=0; 3y=9; y=9/3; y₂=3
Проверка:
при x₁=10/3 и y₁=15
(10/3 -2)²+(15-6)²=97/9
(10/3 -6/3)²+81=97/9
9·16/9+9·81=97 - равенство не выполняется, так как уже 9·81>97, следовательно, корень y₁ к данной системе вообще не подходит;
при x₁=10/3 и y₂=3
(10/3 -2)²+(3-6)²=97/9
9·16/9 +9·9=97
16+81=97- равенство выполняется;
при x₂=-2 и y₂=3
(-2-2)²+(3-6)²=97/9
9(16+9)=97
9·25≠97 - равенство не выполняется, так как 9·25>97.
Отсюда следует, что единственными корнями являются:
x₁=10/3=3 1/3 и y₂=3.
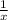, за 24 дня второй выполнит 24·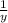
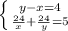
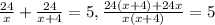
!) а в квадр..> или = 0. Умножим обе части неравенства на 5 и прибавим 1. 5а в квадр..>0; 5а в квадр.+1> или = 1; 5а в квадр.. > или = Нет! Не так Рассмотрим разность: 5а в квадр.+1)-5а вквадр.=1, 1.>0 Следовательно, 5а в квадр. +1 больше5а в квадр. Всё! б) (2а-1)(2а+1)=4а в квадр.-1 . Рассмотрим разность между левой и правой частями: 4а в квадр.-(4а в квадр,-1)=4а в квадр-4а в квадр.+1=1. Т. К. !>0, то 4а в квадр больше (2а+1)(2а-1) верно Ч.Т.Д.