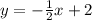Чтобы представить данный одночлен 125d^18 в виде куба некоторого одночлена, мы должны найти корень кубический из этого одночлена. Для этого, мы найдем корень кубический из коэффициента и корень кубический из переменной.
1. Коэффициент 125 - это 5^3, так как 5 * 5 * 5 = 125. Значит, мы можем вынести 5 за скобку и оставить 25d^18.
2. Теперь посмотрим на переменную d. Чтобы найти корень кубический из d^18, мы должны поделить показатель степени на 3. В данном случае, 18/3 = 6. Значит, мы можем вынести d^6 из под корня и оставить d^6 за скобку.
Итак, мы представляем данный одночлен 125d^18 в виде куба некоторого одночлена как (5d^6)^3. Это означает, что мы возведем 5d^6 в куб и получим 125d^18.
Для решения этой задачи нам понадобится использовать формулу комбинаторики, называемую формулой сочетаний. Формула сочетаний выглядит следующим образом:
C(n, k) = n! / (k! * (n - k)!)
Где n - общее количество элементов, а k - количество элементов, которые мы хотим выбрать.
В данном случае у нас имеется 15 деталей и мы хотим выбрать 4 детали. Поэтому в формулу работы комбинаторики подставим значения n = 15 и k = 4:
y=kx+b
b - отвечает за Оу. На графике это (0;2)
kx - отвечает за Ох. На графике это (4;0)
Тогда
0=4k+2
-4k=2
k= -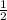
ответ: