Решите с объяснением. первая труба наполняет резервуар на 12 минут дольше, чем вторая. обе трубы наполняют этот же резервуар за 8 минут. за сколько минут наполняет этот резервуар одна вторая труба решите с объяснением.
Пусть t - время заполнения резервуара 1-ой трубой,тогда (t-12) - время заполнения резервуара 2-ой трубой.
В таких задачах площадь резервуара или обьём(неважно) можно брать за 1. Если брать какую-нибудь букву то она потом всёравно сократится. Просто принято брать за 1.))
Пусть 1 - площадь резервуара, тогда cкорость заполнения резервуара 1-ой трубой, скорость заполнения 2-ой трубой. А двумя трубами вместе - или +. Прировняем:
Одна треть, Вам верно посчитали. . Вероятность равна 2*С (2,2)*С (2,0)/C(2,4)=2*1*1/6=1/3 - это используя комбинаторику. Но можно посчитать и исходя из классического определения вероятности. Каким можно вынуть два шара одного цвета? Либо кк, либо сс. Вероятность вынуть первый красный 2/4=1/2 (красных два шара из четырех) , вероятность вынуть второй красный 1/3 (один красный из оставшихся трех) , вероятность вынуть два красных равна произведению вероятностей этих событий (потому что эти события должны произойти одновременно - вероятность совпадения событий равна произведению вероятностей каждого отдельного события! ) 1/2*1/3=1/6. Вероятность вынуть ДВА СИНИХ точно такая же 1/6 (рассуждения те же, только вместо красных - синие) . А вероятность вынуть два шара одного цвета, то есть либо 2 красных, либо 2 синих, равна сумме вероятностей этих событий (поскольку нам достаточно, чтобы произошло ОДНО из ЭТИХ несовместных, то есть не могущих произойти одновременно, событий!) , то есть 1/6+1/6=2/6=1/3. ответ от решения, естественно, не изменяется. Потому что оба решения - ПРАВИЛЬНЫЕ!
Пусть скорость велосипедиста - Х км/ч, тогда скорость автомобилиста - Х +110 км/ч,
велосипедист проехал расстояние от пункта А в пункт В за 60/Х ч, а автомобилист проехал это расстояние за 60/(Х +110) ч, Т.к. по условию велосипедист прибыл в пункт В на 5,5 часов позже автомобилиста, значит время велосипедиста на 5,5 ч больше времени автомобилиста, т.е.
Пусть t - время заполнения резервуара 1-ой трубой,тогда (t-12) - время заполнения резервуара 2-ой трубой.
В таких задачах площадь резервуара или обьём(неважно) можно брать за 1. Если брать какую-нибудь букву то она потом всёравно сократится. Просто принято брать за 1.))
Пусть 1 - площадь резервуара, тогда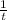 cкорость заполнения резервуара 1-ой трубой,
cкорость заполнения резервуара 1-ой трубой,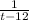 скорость заполнения 2-ой трубой. А двумя трубами вместе -
скорость заполнения 2-ой трубой. А двумя трубами вместе - 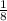 или
или 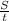 +
+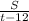 . Прировняем:
. Прировняем:
t=24 - время заполнения 1-ой трубой
t=24-12=12 - время заполнения 2-ой трубой.