Question

Найти неопределенные интегралы: $\int\limit {\frac{sinx}{1+3cos2x}} \, dx$

$\int\limit {\frac{3x+13}{(x-1)(x^2+2x+5)}} \, dx$

Answer 1

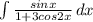
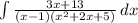
$1)\ \ \int \dfrac{sinx}{1+3cos2x}\, dx=\int \dfrac{sinx\, dx}{1+3(2cos^2x-1)}=\int \dfrac{sinx\, dx}{6cos^2x-2}=\int \dfrac{sinx\, dx}{2\, (3cos^2x-1)}=\\\\\\=-\dfrac{1}{2\sqrt3}\int \dfrac{d(\sqrt3cosx)}{(\sqrt3\, cosx)^2-1}=\Big[\ u=\sqrt3cosx\ ,\ du=-\sqrt3sinx\, dx\ \Big]=-\dfrac{1}{2\sqrt3}\int \dfrac{du}{u^2-1}=\\\\\\=-\dfrac{1}{2\sqrt3}\cdot \dfrac{1}{2}\cdot ln\Big|\dfrac{u-1}{u+1}\Big|+C=-\dfrac{1}{4\sqrt3}\cdot ln\left |\dfrac{\sqrt3\, cosx-1}{\sqrt3\, cosx+1}\right |+C$

$2)\ \ \int \dfrac{3x+13}{(x-1)(x^2+2x+5)}\, dx=I\\\\\\\dfrac{3x+13}{(x-1)(x^2+2x+5)}=\dfrac{A}{x-1}+\dfrac{Bx+C}{x^2+2x+5}\\\\\\3x+13=A(x^2+2x+5)+(Bx+C)(x-1)\\\\x=1:\ \ A=\dfrac{3x+13}{x^2+2x+5}=\dfrac{3\cdot 1+13}{1^2+2\cdot 1+5}=\dfrac{16}{8}=2\\\\\\3x+13=Ax^2+2Ax+5A+Bx^2-Bx+Cx-C\\\\\\x^2\ |\ 0=A+B\ \ \ \ ,\ \ \ \ \ \ \ \ B=-A=-2\\x^1\ |\ 3=2A-B+C\ \ ,\ \ \ 3=4+2+C\ ,\ \ C=-3\\x^0\ |\ 13=5A-C$

$I=\int \dfrac{2}{x-1}\, dx+\int \dfrac{-2x-3}{x^2+2x+5}\, dx=2\, ln|x-1|-\int \dfrac{2x+3}{(x+1)^2+4}\, dx=\\\\\\=2\, ln|x-1|-2\int \dfrac{x\, dx}{(x+1)^2+4}-3\int \dfrac{dx}{(x+1)^2+4}\ ;$

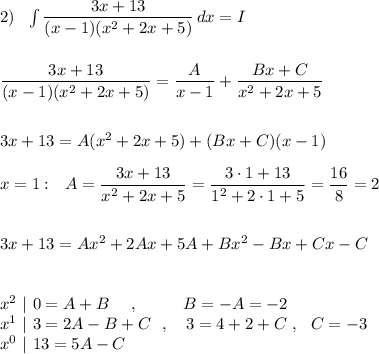
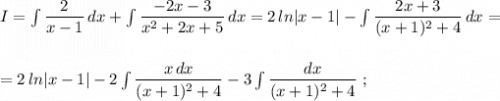
$\star \ \ \int \dfrac{x\, dx}{(x+1)^2+4}=\Big[\ t=x+1\ ,\ x=t-1\ ,\ dx=dt\ \Big]=\int \dfrac{(t-1)\, dt}{t^2+4}=\\\\\\=\dfrac{1}{2}\int \dfrac{2t\, dt}{t^2+4}-\int \dfrac{dt}{t^2+2^2}=\dfrac{1}{2}\cdot ln |\, t^2+4\, |-\dfrac{1}{2}\cdot arctg\dfrac{t}{2}+C=\\\\\\=\dfrac{1}{2}\cdot ln\Big|\, x^2+2x+5\, \Big|-\dfrac{1}{2}\cdot arctg\dfrac{x+1}{2}+C_1\ ;\\\\\\\star \int \dfrac{dx}{(x+1)^2+4}=\dfrac{1}{2}\cdot arctg\dfrac{x+1}{2}+C_2\ ;$

$I=2\, ln|x-1|-2\cdot \Big(\dfrac{1}{2}\cdot ln\Big|\, x^2+2x+5\, \Big|-\dfrac{1}{2}\cdot arctg\dfrac{x+1}{2}+C_1\Big)-\\\\\\-\dfrac{3}{2}\cdot arctg\dfrac{x+1}{2}+C_2\ ;\\\\\\\\I=2\ln |x-1|-ln|x^2+2x+5\, |-\dfrac{1}{2}\, arctg\dfrac{x+1}{2}+C$